日本応用数理学会
2016年度 年会
プログラム
ver. 2016-09-07
ご注意:本プログラムは暫定版であり変更される可能性があります.
9月11日
9月12日
9月13日
9月14日
▷ 総合講演 @ メインホール [9月13日:15:00-16:50:メインホール](座長:[前半]梶原 健司(九州大学),[後半]大石 進一(早稲田大学))
- 楕円モジュラーj-関数—三幅対の夢 / ○金子 昌信 (九州大学 大学院数理学研究院) [概要]
楕円モジュラー 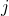 -関数はモジュラー関数の中でも最も基本的な関数である. これについて,虚数乗法論,そして Monstrous Moonshine という大きな理論が知られている. それらをおおざっぱに,それぞれ
-関数はモジュラー関数の中でも最も基本的な関数である. これについて,虚数乗法論,そして Monstrous Moonshine という大きな理論が知られている. それらをおおざっぱに,それぞれ 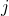 -関数の虚二次点,無限遠点での振る舞いに関して何かを言う理論だと思うとすると,もう一つ,実二次点での振る舞いはどうかというのが気になる. これらについて筆者が20年来行ってきたささやかな研究,空想についてお話ししたいと思う.
-関数の虚二次点,無限遠点での振る舞いに関して何かを言う理論だと思うとすると,もう一つ,実二次点での振る舞いはどうかというのが気になる. これらについて筆者が20年来行ってきたささやかな研究,空想についてお話ししたいと思う.
- 未来を拓く 北九州市から地方創生の成功モデルを / ○大川 博己 (北九州市産業経済局 企業誘致(特命)担当理事)
(総合講演終了後)
▷ 若手・女性研究者ランチミーティング [9月14日:12:20-13:30:2B]
[概要]若手研究者による2件のチュートリアルに加え,キャリアパスやワークライフバランスなど,若手・女性研究者が日ごろ気になっていることを,多くの方と共有し,情報交換を行う時間も設けました。最初の取り組みですので,若手や女性に限らず多くの方に参加していただき,ざっくばらんに,様々な思いを話す機会としたいと考えています。それをもとに,今後,個人としてまたは学会として,どのようなことが出来るのかを模索したいと思います。少しばかりの軽食やお菓子をご用意してお待ちしております。
- 交通流の数理-数理モデルでの表現・解析・理解・発展 / ○友枝 明保(武蔵野大学工学部数理工学科) [概要]
交通流研究の一つのゴールは,交通渋滞を解消する方策を導くことである.本チュートリアルでは,交通流研究の流れに沿って,現象を表現する数理モデルの構築からスタートし,数理モデルの解析を通じた現象の理解,さらには,渋滞を解消する方策など,数理モデル研究から得られた知見について概観する.
- 離散可積分系によるビッグデータ解析 / ○木村欣司(京都大学大学院情報学研究科数理工学専攻)
[概要]
ビッグデータ解析において、主成分分析は重要な道具の一つであり、それを実行する上で、Thick restart Golub-Kahan-Lanczos(TRGKL)法は、有用である。TRGKL法には、上2重対角行列の特異値分解を複数回解くフェーズがあり、QR法、分割統治法、直交QD法、2分法、dqds法、逆反復法、MRRR法などを用いる。直交QD法とdqds法は、離散可積分系と解釈できるため、離散可積分系の知識を利用した実装が可能である。単体のアルゴリズムの比較実験に加え、TRGKL法にQR法または直交QD法を組み込んだ場合の比較実験の結果も紹介する。
▷ [JSIAM-ANZIAM 特別OS] 応用可積分系 (1) [9月12日:09:30-10:50:2B](座長:梶原 健司(九州大学マス・フォア・インダストリ研究所))
- The 3D complex Burgers equation, equivalent to linear Schrödinger equation / ○Broadbridge Philip (La Trobe University) [概要]
The 3d complex Burgers equation is related to the linear Schrodinger equation by the Hopf- Cole transformation that is usually applied to the linear heat equation. Although it is closely related to Madelung's 1927 hydrodynamic picture of quantum mechanics, the complex Burgers formulation has particular advantages. For example the total particle energy is a classical expectation of 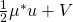 . It also suggests an extension of the wave function to a 4-potential.
. It also suggests an extension of the wave function to a 4-potential.
- Integrable motion of space curve and its determinant expressions / ○Ohta Yasuhiro (Kobe University) [概要]
Integrable motion of space curve is explicitly described by determinant solutions of two-component KP hierarchy.
- Integrable self-adaptive moving mesh schemes for nonlinear waves / ○丸野 健一 (早稲田大学理工学術院) [概要]
Integrable self-adaptive moving mesh schemes for nonlinear wave equations
give a powerful tool for numerical computation of nonlinear waves. An important key of construction of self-adaptive moving mesh schemes is a discretization of hodograph transformation and discrete conservation laws. We show systematic methods to construct integrable self-adaptive moving mesh schemes and a relationship of a motion of discrete curves.
▷ [JSIAM-ANZIAM 特別OS] 応用可積分系 (2) [9月12日:11:00-12:20:2B](座長:梶原 健司(九州大学マス・フォア・インダストリ研究所))
- Invariant measures, volumes and random lattices / ○Forrester Peter (University of Melbourne) [概要]
The invariant measures on the classical matrix groups 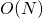 and
and 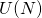 were introduced by Hurwitz in a foundational paper in 1897. A subsequent development was by Siegel in the mid 40's who introduced an invariant measure on SL
were introduced by Hurwitz in a foundational paper in 1897. A subsequent development was by Siegel in the mid 40's who introduced an invariant measure on SL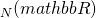 in the context of a study of the geometry of numbers. Later Duke, Rudnik and Sarnak applied Siegel's invariant measure to the asymptotic computation of the number of matrices in SL
in the context of a study of the geometry of numbers. Later Duke, Rudnik and Sarnak applied Siegel's invariant measure to the asymptotic computation of the number of matrices in SL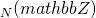 , with a bounded norm. In this talk these lines of study will be reviewed, and some new results relating to the geometry of random lattices will be presented.
, with a bounded norm. In this talk these lines of study will be reviewed, and some new results relating to the geometry of random lattices will be presented.
- Recent developments in integrable algorithms / ○Nakamura Yoshimasa (Kyoto University) [概要]
Integrable dynamical systems originally appear in classical mechanics and have rich
applications to various branches in mathematics as well as in mathematical physics.
Numerical analysis is one of such fields. Recurrence relations of some existing
numerical algorithms are equivalent to discrete-time integrable systems themselves
having explicit solutions and many conserved quantities. They are classified into three
classes.
1) matrix eigenvalue algorithms (e.g. qd algorithm vs. discrete time Toda lattice)
2) convergence acceleration algorithms through continued fractions (e.g. epsilon
algorithm vs. discrete time potential KdV)
3) algorithms based on additional formulas (e.g. arithmetic-geometric mean algorithm
of Gauss)
Conversely, a time discretization of some integrable system may contribute to design a
new effective numerical algorithm. A notion of “integrable algorithms” is then
introduced.
In this talk I will speak about some recent development in integrable algorithms.
- Polynomial degree growth in integrable lattice equations and their reductions / ○Roberts John (University of New South Wales) [概要]
A key detector for a partial difference equation or lattice equation to be integrable relates to how the degree of an indeterminate inserted in the boundary values grows sub-exponentially as the equation is propagated. We review some recent joint work with Dinh Tran that proposes an exact formula for this degree for a large class of (non-autonomous) lattice equations. A consequence is quadratic degree growth for “repeating” staircase reductions of such lattice equations.
- Coprimeness condition as an algebraic reinterpretation of singularity confinement / ○時弘 哲治 (東京大学大学院数理科学研究科) [概要]
coprimeness とは,離散有理写像が格子点上でとりうる値を初期値の有理式とみたとき,一定の距離以上離れると,互いに素となる性質である.これは,特異点閉じ込めの概念を代数的に再定義したものと考えられ,coprimeness条件を用いて,「特異点閉じ込め」の成り立つ高次元の系を定義できる.本講演では,可積分力学系とカオス力学系の双方の性質を兼ね備えた系(準可積分系)の代数的エントロピーやco-primenessについて最近の研究成果について報告する.準可積分系であるHietarinta-Viallet方程式およびその拡張に対して代数的エントロピーを厳密に求め,準可積分な2次元格子系(dKdV方程式の拡張)を定義し,co-primenessが成立すること,その簡約が準可積分系の階層構造を与えること,また,2+1次元の擬戸田方程式の導出とその性質などについて説明する.
▷ [JSIAM-ANZIAM 特別OS] 応用力学系 (1) [9月13日:09:30-10:50:2B](座長:國府 寛司(京都大学・大学院理学研究科))
- [30分講演] Failure of structures: can you see it coming? / ○Hinke Osinga (University of Auckland, New Zealand) [概要]
Failure of structures in an earthquake is an important problem that is still not well understood. Design specifications use guidelines that are based on the magnitude of an earthquake, among other things. We investigate how an external force with varying magnitudes and principal frequencies affects a planar, post-tensioned frame. We use a boundary-value-problem approach to compute the failure boundary directly and determine its nature. This shows that inherent nonlinearities in the system can have dramatic effects on structural stability, especially when the structure has a natural frequency close to that of the external forcing.
- [30分講演] The canard phenomenon in aircraft ground dynamics / ○Bernd Krauskopf (University of Auckland, New Zealand), James Rankin (University of Exeter, United Kingdom), Mathieu Desroches (INRIA Sophia-Antipolis, France), Mark Lowenberg (University of Bristol, United Kingdom) [概要]
We show that the sudden loss of lateral stability of a mid-size passenger aircraft turning on the ground is due to the multiple-time-scale phenomenon known as a canard explosion.
- Estimation of mean squared error of beta-encoders through their dynamical zeta functions / ○Shinohara Katsutoshi (Hitotsubashi University) [概要]
A beta-encoder is an analog-to-digital(A/D)-converter based on the beta-expansion, that is, the expansion of real numbers with non-integer bases. It is proposed that the beta-encoders exhibit better performance than the conventional binary A/D converters. A theoretically challenging problem is to give rigorous estimates of the mean squared error of beta encoders: such a problem is by no means easy due to the chaotic behavior of corresponding dynamical systems. In this talk, I propose a method of estimating their upper bound through the analysis of the dynamical zeta function of corresponding systems.
▷ [JSIAM-ANZIAM 特別OS] 応用力学系 (2) [9月13日:11:00-12:20:2B](座長:國府 寛司(京都大学・大学院理学研究科))
- [30分講演] Transonic canards and stellar winds / ○Martin Wechselberger (School of Mathematics & Statistics, University of Sydney, Australia) [概要]
Looking at the gas dynamics of stars under the assumption of spherical symmetry, I will show that transonic events in such systems are canard phenomena — peculiar solution structures identified in geometric singular perturbation problems. Consequently, stellar winds are carried by `supersonic ducks', and canard theory provides a mathematical framework for this astrophysical phenomenon.
This is collaborative work with Paul Carter (Brown) and Edgar Knobloch (UC Berkeley).
- [30分講演] Pulse generators / ○Nishiura Yasumasa (Tohoku University), Yadome Masaaki, Teramoto Takashi (Asahikawa Medical University) [概要]
We study a spontaneous pulse-generating mechanism in an excitable medium with jump-type heterogeneity.
Such a pulse generator (PG) has attracted considerable interest due to the computational potential
of pulse waves in physiological signal processing. We first investigate the conditions for the onset
of robust-type PGs, and then we show the global bifurcation structure of heterogeneity-induced
patterns, including the complex ordered sequence of pulse-generating manners. We devise numerical
frameworks to trace the long-term behavior of PGs as periodic solutions, and we detect the associated
terminal homoclinic orbits that are homoclinic to a special type of heterogeneity-induced ordered
pattern with a hyperbolic saddle. These numerical approaches assist us in identifying a candidate
for the organizing center, and producing a variety of PGs as a codimension-two gluing bifurcation,
in which two homoclinic trajectories associated with pulse emission and breathing motions form a
butterfly configuration.
- Weighted Birkhoff Average and Quasiperiodicity / Suddhasattwa Das (University of Maryland), ○Yoshitaka Saiki (Hitotsubashi University), Evelyn Sander (George Mason University), James A. Yorke (University of Maryland) [概要]
Our small modification of numerical Birkhoff averages significantly speeds the convergence rate for quasiperiodic trajectories. The method and its applications are shown in this talk.
▷ [正会員主催OS] FreeFem++の開発と利用 [9月12日:09:30-10:50:1A](座長:大塚 厚二(広島国際学院大学))
- [40分講演] Dissection 直接法並列解法とFreeFem++での活用 / ○鈴木 厚 (大阪大学サイバーメディアセンター) [概要]
有限要素法解析に現れる大規模疎行列の並列直接法ソフトウェア Dissection を開発した. 非零成分が構造対称となる非対称行列で, 対称軸選択によりLDU分解可能なものを扱う. nested-dissection オーダリングにより効率的な並列計算を実現する. また行列が特異な場合でも, 核の次元を数値的に決定し, 像空間に解を求める. FreeFem++ の線形ソルバーを動的なライブラリー結合の機能により置き換えることで, マルチコアCPUでの並列計算を実行する.
- Shape Optimization Method for Flow Stability Control and its application toward Hemodialysis / ○中澤 嵩 (東北大学大学院情報科学研究科) [概要]
講演者がこれまで構築してきた,形状最適化問題を活用することによる流れの安定制御について講演する.具体的には,目的関数に散逸エネルギーを,主問題に定常Navier-Stokes方程式を定義した場合の最適化問題を解き,その後に線形安定性解析を行うことで初期形状と最適形状における安定性を比較する.また,このような手法を用いて,人工血管の最適設計に応用したので,この内容についても報告する.
- 放熱量最大化を目的とした非定常自然対流場の形状最適化 / ○片峯 英次 (岐阜工業高等専門学校), 石井 航平 (豊橋技術科学大学(学生)), 今井 伸哉 (長岡技術科学大学(学生)) [概要]
非定常の自然対流場に対して,熱伝達境界おいて放熱量を最大化する形状最適化問題を取りあげて,その解法を紹介する.問題を定式化し,随伴変数法を利用して形状修正の感度となる形状勾配密度関数を導出した.導出した感度に基づいて力法(あるいは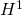 勾配法)を適用し,Freefem++を利用して解析した数値解析結果を紹介する.
勾配法)を適用し,Freefem++を利用して解析した数値解析結果を紹介する.
▷ [正会員主催OS] 先進的環境おける数値計算と関連基盤技術 (1) [9月12日:09:30-10:50:3E](座長:深谷 猛(北海道大学))
- 高バンド幅メモリ環境における数値計算アルゴリズムの変革と自動チューニング技術~FDMコードを例にして~ / ○片桐 孝洋 (名古屋大学情報基盤センター), 松本 正晴 (東京大学情報基盤センター), 大島 聡史 (東京大学情報基盤センター) [概要]
本発表では、ポストムーア時代では計算性能から相対的にメモリ性能が向上することを仮定し、高バンド幅メモリ環境での数値計算アルゴリズムの変革の可能性と自動チューニング技術(AT)について述べる。特に、有限差分法(FDM)コードにおけるAT適用の事例について、3次元積層技術による高バンド幅メモリをもつスパコンでの性能評価結果を紹介する。
- 複数性能パラメタ空間を線形探索する標本点逐次追加型性能パラメタ推定法 / ○望月 大義 (工学院大学), 藤井 昭宏 (工学院大学), 田中 輝雄 (工学院大学) [概要]
ソフトウェア自動チューニングの手法の1つに標本点逐次追加型性能パラメタ推定法がある.この手法では複数の性能パラメタを同時に推定する場合に推定コストが著しく増加することが課題である.この課題を解決するために,複数の性能パラメタを一次式として定式化し,一次式であらわした性能パラメタを推定する方法を繰り返し行う手法を提案する.さらに,複数の性能パラメタ間の相関を用いて探索を効率化する.
- 並列FFTにおける通信隠蔽の自動チューニング / ○高橋 大介 (筑波大学) [概要]
本論文では,並列FFTにおける通信隠蔽の自動チューニング手法について述べる.
並列FFTにおいては,全対全通信が実行時間の多くを占めることが知られている.
並列FFTの実行時間を削減するためには,演算と通信をオーバーラップさせることにより,通信時間を隠蔽することが有効である.
通信時間の隠蔽に関しては,さまざまなパラメータが存在するが,最適なパラメータを自動チューニングにより最適化する手法を提案する.
マルチコア超並列クラスタにおける性能評価の結果についても報告する.
- 時間並列計算法の課題とその解決に関する研究 / ○飯塚 幹夫 (理化学研究所 計算科学研究機構), 小野 謙二 (九州大学 情報基盤研究開発センター) [概要]
ポストペタ時代の計算資源は,アプリケーションに対し現状に比べさらに数桁上の並列性を要求する見通しである.そのような中,時間軸を新しい並列軸として利用する時間並列計算法が期待され,2001年に実用的なParareal 法が提案されて以降研究開発が活発となっている.Parareal法も多くの課題を抱えているが,その課題解決の手法も多数提案されている.本講演では、現在実施中の課題解決の研究について紹介する。
▷ [正会員主催OS] 先進的環境おける数値計算と関連基盤技術 (2) [9月12日:11:00-12:20:3E](座長:片桐 孝洋(名古屋大学))
- クラスタ型ヘテロジニアス環境におけるタイルQR分解 / ○高柳 雅俊 (山梨大学大学院), 鈴木 智博 (山梨大学大学院) [概要]
近年、CPUとGPUを搭載したクラスタ型スーパーコンピュータが多数登場してきている。しかし、このヘテロジニアスクラスタシステム向けに開発された数値計算ライブラリはまだない。今回、タイルQR分解をTUBAME2.5上に実装した。発表では、実装方法や実験による性能評価について報告する。
- ◎AVX2を用いた倍々精度演算の反復解法への適用と評価 / ○菱沼 利彰 (筑波大学) [概要]
高精度演算を用いれば,Krylov部分空間法の収束が改善できる.
倍々精度演算は,倍精度演算を組み合わせて4倍精度演算を実行する手法である.
我々はSIMD拡張命令AVX2や疎行列の格納形式であるBCRS4x1形式を用いて,倍々精度ベクトル演算や倍精度疎行列と倍々精度ベクトルの積,およびその転置行列に対する積を高速化している.
本発表では,これらをKrylov部分空間に適用した際の性能を示し,倍精度演算と比較したDD演算の性能を評価する.
- XeonPhi上での乗法シュワルツ-ブロック化多色順序付けGS法を適用したSA-AMGの性能評価 / ○河合 直聡 (東京大学 情報基盤センター), 伊田 明弘 (東京大学 情報基盤センター), 岩下 武史 (北海道大学 情報基盤センター), 中島 浩 (京都大学 学術情報メディアセンター) [概要]
本発表では代数マルチグリッド法を対象としてマルチコア、メニーコア上で高い性能を出すことができるスムーザの提案を行う。評価は汎用のマルチコアおよびXeonPhiのKNC、KNL上で行い、その結果について述べる。
- マルチコア・メニーコア環境における反復型ステンシル計算と時空間タイリング / ○深谷 猛 (北海道大学), 岩下 武史 (北海道大学) [概要]
反復型ステンシル計算は科学技術計算に頻繁に現れる計算パターンのひとつであり,メモリバンド幅に性能が律速されることが知られている.メモリからのデータ転送コストを削減するための手法として時空間タイリングが有名であるが,タイリングを施すことでタイル間の依存関係が発生し,多数のスレッドを効率的に活用することが難しくなる場合がある.本発表では,簡単なステンシルに関して,いくつかのタイリング手法を適用し,それらの性能評価・比較を行う.
▷ [正会員主催OS] 多倍長精度浮動小数点演算の高速化手法と応用 (1) [9月12日:13:30-14:50:2B](座長:中里 直人(会津大学))
- 任意精度浮動小数点演算環境における行列積チューニングの試行 / ○幸谷 智紀 (静岡理工科大学) [概要]
現在の高速な計算機環境では,MPFR/GMPのようなソフトウェアによる任意精度浮動小数点演算も,比較的桁数が少ない場合はキャッシュメモリのヒット率の影響を受けやすい。本講演ではMPFR/GMPを用いて実装した行列積計算をブロック化し,計算桁数ごとに可能な限り高速化した結果について報告する。
- ◎4倍精度固有値ソルバライブラリQPEigenKの京コンピュータにおける性能分析 / ○廣田 悠輔 (理化学研究所計算科学研究機構), 山田 進 (日本原子力研究開発機構システム計算科学センター), 今村 俊幸 (理化学研究所計算科学研究機構), 佐々 成正 (日本原子力研究開発機構システム計算科学センター), 町田 昌彦 (日本原子力研究開発機構システム計算科学センター) [概要]
我々は4倍精度標準固有値ソルバライブラリQPEigenKを開発している.
本講演では,QPEigenKの京コンピュータ上での性能の分析結果について報告する.
また,将来の計算機において固有値ソルバが直面すると予想される性能上の問題についても述べる.
- 多倍長精度浮動小数点演算を用いた実数計算ライブラリの実現方式 / ○川端 英之 (広島市立大学) [概要]
浮動小数点演算による数値計算においてはユーザは計算結果の正確さに敏感であることが要求される.これに対し我々は,数値表現の詳細を意識せずとも任意の精度の計算結果を得ることを可能にする実数計算ライブラリを開発している.実数計算ライブラリの実現方式には様々なものが考えられるが,本発表では,多倍長精度浮動小数点演算を用いて任意精度の計算を実現する手法について,幾つかの試みを紹介する.
- 中心値・半径方式による精度保証付き多倍長区間演算ライブラリの開発 / ○松田 望 (電気通信大学 情報理工学研究科) [概要]
我々は、新しい精度保証付き多倍長区間演算ライブラリを開発している。
本ライブラリの特徴は、区間を中心値と半径の組み合わせで表現することである。
旧バージョンの実装によって、この設計の優位性を確認できたが、計算速度は遅かった。
新バージョンでは、 MPFR を組み込むことによって、高速化を図っている。
新バージョンはまだ未完成だが、既に区間乗算において、既存のライブラリを上回る速度を実現している。
▷ [正会員主催OS] 多倍長精度浮動小数点演算の高速化手法と応用 (2) [9月12日:15:00-16:20:2B](座長:湯浅 富久子(高エネルギー加速器研究機構))
- 多倍長計算が開く格子QCDの新しい可能性 / ○中村 純 (理化学研究所), 岡 将太郎 (立教大学) [概要]
スーパーコンピュータはその高い数値演算性能により、素粒子・原子核の研究の強力な道具となっている。本講演では、多倍長計算がこれまで不可能と思われていた計算を可能にし、素粒子・原子核研究の新しい地平が明らかにありつつある状況を報告する。
- SIMD命令を用いた整数除算の高速化 / ○高橋 大介 (筑波大学) [概要]
本論文では,SIMD命令を用いた整数除算の高速化について述べる.
多倍長精度浮動小数点演算を整数演算によって実現する場合,整数演算の性能が多倍長精度浮動小数点演算の性能を大きく左右する.
多くのプロセッサでは整数加減乗算のSIMD命令がサポートされているが,整数除算のSIMD命令をサポートしているプロセッサはほとんど存在しないのが現状である.
そこでSIMD命令を用いて整数除算を高速化する手法を提案する.
また,SIMD命令を搭載したプロセッサにおける性能評価の結果についても報告する.
- ◎GMPを用いた混合精度型プログラムの自動生成機構の提案 / ○菱沼 利彰 (筑波大学), 藤井 昭宏 (工学院大学), 田中 輝雄 (工学院大学), 平澤 将一 (東北大学) [概要]
GMPライブラリを用いた任意多倍長精度のプログラムは,コードのほとんどを手続きの形式で記述する必要があり,一般的な倍精度のCコードを多倍長精度に書き換えるには高い実装コストを必要とする.
本研究では,アルゴリズムの精度依存性を手軽に検証するために,プログラムに対象とする精度や変数を指定するディレクティブを記述するだけで,GMPを用いた任意多倍長精度の混合精度型プログラムを自動生成する機構を提案する.
- 多倍長精度積分計算を加速させる専用システムの開発とその応用II / ○台坂 博 (一橋大学), 中里 直人 (会津大学), 石川 正 (高エネルギー加速器研究機構), 湯浅 冨久子 (高エネルギー加速器研究機構), 似鳥 啓吾 (理化学研究所計算科学研究機構) [概要]
科学技術計算において高精度計算の必要性が増している。
我々は、高精度演算かつ高速計算が可能な、再構成可能デバイス(FPGA)による専用アクセラレータとコンパイラを含む開発環境からなる
専用計算システムの開発を進めている。
このシステムの応用として、素粒子物理学での場の理論による高次摂動までの補正効果を取り入れる数値計算に取り組んでいる。そこでは、特異性を有するファインマンループ図形積分が現れるが、この多次元数値積分を事例として多倍長演算の有効性と専用計算システムの性能評価を行っている。
専用計算システムは更なる開発が進められており、
専用アクセラレータの増強による計算能力の改善、
コンパイラのMPIコード生成機能の追加、
OpenCLによるGPUでの4倍精度計算化
を行った。
本講演では専用計算システムの現状と新たに行っているファインマンループ図形積分の計算例について報告する。
▷ [正会員主催OS] マテリアルズインフォマティクスと応用数理(1) [9月14日:09:30-10:50:2C](座長:高田 章(旭硝子))
- [15分講演] 趣旨説明とマテリアルズインフォマティクスプロジェク トの紹介 / ○伊藤 聡 (JST) [概要]
物質・材料の研究おいて、これまでの物質科学に基づくものではなく、材料データを基礎とする新しい手法「マテリアルズ・インフォマティクス」が注目を集めている。これは大規模なデータを集めることができるようになったこと、最適化や推定手法、AI技術など情報科学的な学問の進展などを背景としている。本発表ではその概要を説明するとともに、国内外の動向を紹介する。
- [30分講演] ベイジアンアプローチに基づく情報統合型物質・材料探索 / ○吉田 亮 (統計数理研究所) [概要]
物質探索や材料設計のパラメータ空間は極めて広大である。例えば、低分子有機化合物のケミカルスペースには、およそ10^60個の埋蔵分子が存在すると言われている。物質探索や材料設計の本質は、このような広大な空間から所望の物性・機能を併せ持つ仮説構造を発掘することである。これは多目的最適化の問題である。講演では、この問題を解くための有効な手段であるベイジアンアプローチに基づく物質探索手法について解説する。
- [30分講演] 機械学習による粒界データ解析 / ○烏山 昌幸 (名古屋工業大学,国立研究開発法人物質・材料研究機構,JSTさきがけ), 田村 友幸 (名古屋工業大学,国立研究開発法人物質・材料研究機構), 小林 亮 (名古屋工業大学,国立研究開発法人物質・材料研究機構), 竹内 一郎 (名古屋工業大学,国立研究開発法人物質・材料研究機構), 中山 将伸 (名古屋工業大学,国立研究開発法人物質・材料研究機構) [概要]
複数の結晶構造の境界面が作る粒界は電解質材料の抵抗など,材料の性質に多大な影響を与えることが知られているが,その多様性からシミュレーションや実験による網羅的な調査は困難である.本発表では粒界の解析に計算材料科学のデータと機械学習を組み合わせたアプローチへの取り組みを紹介する.
▷ [正会員主催OS] マテリアルズインフォマティクスと応用数理(2) [9月14日:11:00-12:20:2C](座長:伊藤 聡(JST))
- [30分講演] 産業界からの期待 / ○高田 章 (旭硝子(株)) [概要]
マテリアルインフォマティクスに対する産業界からの期待を述べる。
- [30分講演] 材料科学に対する応用数学からの貢献 / ○田上 大助 (九州大学) [概要]
数値計算手法の効率や精度を数学の観点から検証することによってより大規模な数値計算が可能になっている例や, 材料物性を理解するために数学の観点からの解析が役立っている例などを通して, 産業界に対する数学からの貢献, および材料科学に対する応用数学からの貢献について述べる.
- [5分講演] まとめ / ○伊藤 聡 (情報・システム研究機構 統計数理研究所) [概要]
▷ [一般講演] 科学技術と数値計算 [9月14日:15:00-16:20:2C](座長:土屋 卓也(愛媛大学))
- 燃料最小化航路計画問題のMISOCP定式化とルート生成アルゴリズム / 田中 未来 (東京理科大学), ○小林 和博 (東京理科大学) [概要]
出発点から到着点に向けて船舶が運航する際,燃料消費量が最小になるような航路及び船速を求める問題を扱う.これを混合整数二次錐最適化問題として定式化し,効率的な解法を提案する.
- ◎コレスキーQR分解に基づく一般化シュティーフェル多様体上のレトラクション / ○相原 研輔 (東京理科大学), 佐藤 寛之 (東京理科大学) [概要]
リーマン多様体上の最適化におけるニュートン法などの反復法では,点列を更新する際に,探索方向に進んだ点を多様体上に写すレトラクションと呼ばれる写像が必要となる.シュティーフェル多様体上ではQR分解に基づくレトラクションがよく用いられるが,それを一般化シュティーフェル多様体上に素朴に拡張したものは多くの計算を必要とする.そこで本講演では,コレスキーQR分解を応用した計算効率の良いレトラクションを提案する.
- 微分値を含む多次元数値積分法 / ○落合 芳博 (近畿大学) [概要]
任意形状領域における多次元数値積分法を発表する.特に,微分値を含む任意分布関数の積分法を示す.本手法は,特異性を含む多次元数値積分を効率的に行うことができる.また,不連続を含む多次元数値積分に効果を発揮する.
- Cauchyの主値積分とHadamard の有限部分積分の数値計算法 / ○平山 弘 (神奈川工科大学) [概要]
Cauchyの主値積分とHadamard の有限部分積分は、解析的な微分法を使う数値的Taylor展開法を使うと、特異性を除去することが容易にできる。このとき生じる見かけ上の特異点もその特異点でTaylor展開することに容易に除去できる。特異性を除去した積分は、数値積分法を使って容易に積分できる。
▷ [一般講演] 機械学習/[一般講演] 位相幾何 [9月12日:11:00-12:20:3F](座長:烏山 昌幸(名古屋工業大学))
- 双対平坦空間における多次元尺度構成法の拡張 / ○熊谷 敦也 (日本大学商学部) [概要]
双対平坦空間は、情報幾何において重要な役割を持っており、構成する点同士の離れの度合はBregmanダイバージェンスとして表される。双対平坦空間においても、特定の点の接空間はユークリッド的であるため、そこで自然に多次元尺度構成法(MDS)を考えることができることは、かつて指摘した通りである。本講演では、接空間におけるMDSを拡張する形でその周りの「曲がり」を取り入れる座標の表式を得たので、これを紹介するとともに、数値計算例を示す。
- ◎非負値行列分解を用いた多層ニューラルネットワークとその並列化 / ○井上 雄登 (筑波大学), 櫻井 鉄也 (筑波大学), 今倉 暁 (筑波大学), 二村 保徳 (筑波大学) [概要]
多層ニューラルネットワーク(NN)は画像認識などの分野において広く用いられている.多層NNでは目的関数の最適化に主に確率的勾配法が用いられるが,学習率の調整が問題となる.提案する非負値行列分解を用いた多層NNでは学習率の調整が不要となり,行列演算をベースとした理論展開が可能となる.本講演では非負値行列分解型の多層NNとその並列実装について述べ,確率的勾配法にもとづく最適化と比較し議論する.
- 量子状態空間の指数型測地線の力学的特徴づけ / ○上野 嘉夫 (京都薬科大学 基礎科学系) [概要]
前回年会や論文(Mathematical Modeling and Geometry 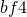 , 19-33 (2016))において,トレース
, 19-33 (2016))において,トレース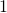 の
の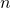 次半正定値エルミート行列(密度行列)のなす量子状態空間
次半正定値エルミート行列(密度行列)のなす量子状態空間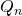 上に拡張されたHebb型学習方程式(EAHLE)のすべての解軌道は指数型測地線であることを示した.本発表では,この逆に相当する結果として,
上に拡張されたHebb型学習方程式(EAHLE)のすべての解軌道は指数型測地線であることを示した.本発表では,この逆に相当する結果として,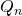 のすべての指数型測地線がEALHEの解軌道の随伴
のすべての指数型測地線がEALHEの解軌道の随伴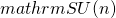 作用変形であるという力学的特徴づけを報告する.これらの軌道と,Moser形式の戸田方程式との関係も報告する.
作用変形であるという力学的特徴づけを報告する.これらの軌道と,Moser形式の戸田方程式との関係も報告する.
- バイオロジカル・モーションの位相幾何学的構造 / ○吉岡 剛志 (帝京平成大学), 山本 知之 (早稲田大学) [概要]
動物の関節などの位置をポイント(点)で表し,そのポイントの動き(モーション)のみを追うことで,人間の脳が“動物の動き”と認識することを“バイオロジカル・モーション”と呼ぶ。この“バイオロジカル・モーション”の構造を,位相幾何学を用いて議論した。
▷ [一般講演] 行列計算 [9月12日:16:30-17:50:2C](座長:保國 惠一(筑波大学))
- ◎逆べき乗法の改善を試みた固有値の反復解法 / ○野村 和史 (大阪大学大学院情報科学研究科情報基礎数学専攻), 降旗 大介 (大阪大学サイバーメディアセンター) [概要]
逆べき乗法のように,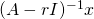 を計算し,これにより得られたベクトルの内積を用いて
を計算し,これにより得られたベクトルの内積を用いて の両隣の固有値を求める手法を提案する.また,それを用いて指定された範囲内に存在する複数の固有値を求める方法も同時に提案する.今回,扱う行列としては対称行列を考えている.
の両隣の固有値を求める手法を提案する.また,それを用いて指定された範囲内に存在する複数の固有値を求める方法も同時に提案する.今回,扱う行列としては対称行列を考えている.
- クリロフ部分空間法のための前処理法の比較について / ○堀端 康善 (法政大学) [概要]
連立1次方程式を解く方法としてクリロフ部分空間法がある.そして,高速化のために前処理を施すことが一般的である.本研究では,その前処理に使う各種前処理行列について,数値実験を行い計算速度を比較する.
- HTS薄膜内遮蔽電流密度解析の高速化 II: QR分解とH行列法の実装 / ○高山 彰優 (山形大学), 齋藤 歩 (山形大学), 神谷 淳 (山形大学) [概要]
クラックを含むHTS薄膜内を流れる遮蔽電流密度の時間発展問題では,各時間ステップで連立1次方程式を解く必要がある.昨年の年会では,同方程式を高速に解くため,ソルバーとしてGMRES法及びH行列法を実装した.本研究では,QR分解を用いた連立1次方程式の高速解法を提案し,同法の性能を述べる.
- ◎不完全HV分解を伴ったCG法の並列計算 / ○鍾 菁廣 (大阪大学サイバーメディアセンター), 小田中 紳二 (大阪大学サイバーメディアセンター) [概要]
並列計算に適した前処理法の研究は重要である. 不完全HV分解を伴った共役勾配法によって, 不完全分解の並列化を実現した. 本公演では, 不完全HV分解による反復解法の収束性の証明と, 共有メモリ構造における並列化効率を評価した. 大阪大学のマルチコア型スーパーコンピュータであるSX-ACEでの解析結果について示す.
▷ [一般講演] 計算幾何/[一般講演] 可積分 [9月14日:13:30-14:50:2C](座長:今井 敏行(和歌山大学))
- 位相的に厳密な円や線分のVoronoi図の統一的近似構成 / ○今井 敏行 (和歌山大学システム工学部) [概要]
線分や円を点列近似し, Voronoi図を近似構成する.計量的な近似性能を省みずに,位相的な厳密性を保証できることを示す.結果として,厳密構成と同等の結果を,個別の構成算法を考案しないで,統一的な手法で,比較的高速に得られることを示す.
- Voronoiベースシミュレーションによる歩きスマホ者が混雑に与える影響の調査 / 小澤 由寛 (青山学院大学理工学部経営システム工学科), ○日吉 久礎 (青山学院大学理工学部経営システム工学科) [概要]
歩行者行動モデルは,通路や建造物の設計のための重要なツールである.近年,筆者らはVoronoi図に基づく歩行者行動モデルを提案した.本研究では,歩きスマホ者が混在する通路において,歩きスマホ者数が通過数に与える影響を,Voronoiモデルを用いて調査する.また,近年採用されつつある,歩きスマホ者と通常歩行者を分離する試みについても,シミュレーションによって調査する.
- 多角形周りの平坦折り紙 / ○山口 大貴 (九州大学大学院数理学府), 川崎 英文 (九州大学大学院数理学研究院) [概要]
単頂点折り紙は、平面上にただ一つの頂点しか存在しない折り紙である。この単頂点折り紙を拡張することを考える。3頂点折り紙から始め、一般のn頂点折り紙として、凸n多角形周りの折り紙を考える。これらの折り紙が平坦可折であるための必要十分条件を考え、その証明を行っていく。
- ◎2元形式の共変式環の斉次根表現を用いた生成元の計算 / ○西田 優樹 (同志社大学大学院理工学研究科), 渡邊 芳英 (同志社大学理工学部) [概要]
2元形式の斉次根からなる多項式をbracketで表したとき,共変式環は正則対称bracket環と同型になることが知られている.そこで,固定した次数の正則bracket多項式全体の線形空間としての基底を構成するアルゴリズムを示し,それを用いて2元形式の共変式環の生成系を具体的に求める.
▷ [一般講演] 常微分方程式 [9月14日:16:30-17:50:2C](座長:小藤 俊幸(南山大学))
- 振動項を含む常微分方程式の数値解法について / ○大野 博 (茨城大学工学部) [概要]
2階常微分方程式の初期値問題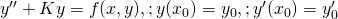 の数値解法について考える。上記の方程式の左辺の2項目の行列
の数値解法について考える。上記の方程式の左辺の2項目の行列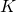 に振動項の振動数
に振動項の振動数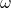 の情報が入っている。この初期値問題の数値解法のAdapted Runge-Kutta-Nystr
の情報が入っている。この初期値問題の数値解法のAdapted Runge-Kutta-Nystr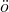 m 法とExtended Runge-Kutta-Nystr
m 法とExtended Runge-Kutta-Nystr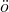 m 法について考える。
m 法について考える。
- アーベル・ボルテラ型積分方程式の数値解法の安定性について / ○小藤 俊幸 (南山大学) [概要]
アーベル・ボルテラ型積分方程式に対する数値解法の安定性を常微分方程式の場合のダルキストのテスト方程式と類似の方程式に基づいて考察する.
- ◎確率ルンゲ・クッタ・チェビシェフ法の数値的安定性の改善 / ○平畠 稜也 (九州工業大学大学院), 小守 良雄 (九州工業大学) [概要]
確率微分方程式の解法の一つにルンゲ・クッタ・チェビシェフ法を埋め込んだSROCKD2法がある。この解法は安定性に優れているが、原点付近で安定領域が欠けるという欠点がある。本研究の目的は、この欠点を取り除くことである。Abdulleらによって提案された、新しいルンゲ・クッタ・チェビシェフ法を用いて、これを行う。発表では、数値実験によって、提案解法の性能を示す予定である。
- 非ホロノミック条件を満たす数値積分法の制御系への適用 / ○岡田 裕佑 (同志社大学大学院) [概要]
微分方程式による非ホロノミック制約条件を持つ制御系に数値積分法を用いる場合,Lagrange-D’Alembertの原理による離散変分法での数値積分法は,系に有効な座標系の導入や数値積分精度を上げるための補完関数により構成が複雑となる.そこで本研究は,直接に非ホロノミック制約条件をハミルトニアン系に含む連立常微分方程式に対し,数値積分法の精度と保存則とみなした非ホロノミック条件保存精度の最適なバランスを考慮した数値解法の試みを報告する.
▷ [一般講演] 数理モデル(1) [9月12日:15:00-16:20:1A](座長:森倉 悠介(早稲田大学))
- 這行ロコモーションにおける動的歩容生成ミニマルモデル / ○黒田 茂 (北海道大学電子科学研究所) [概要]
ムカデやヤスデなど多足動物の脚式這行とミミズやナメクジなどの非脚式這行は、基本的な力学的基盤を共有しており、それらの歩容パターンは体軸方向に伝わる運動波(脚の粗密波や蠕動波等)として観察される。これまでこの運動波の向きは種によって決まっていると考えられてきたが、最近我々により同一種においても波の向きが反転しうることが判明している。本講演では出来るだけ単純な仮定に基づいて構成した動的歩容生成可能な力学的這行モデルを提案する。這行モデルにおける歩容決定メカニズムを摂動的手法と数値解析により考察する。
- ◎放流された内水面水産資源の最適管理戦略に関する数学解析 / ○吉岡 秀和 (島根大学生物資源科学部), 八重樫 優太 (京都大学大学院農学研究科) [概要]
再生産がなく,放流により個体群が維持されている内水面水産資源の動態を常微分方程式系に基づいて記述する.生態学・経済学的な観点から最大化すべき目的関数を設定し,個体群の最適管理戦略を決定するハミルトン・ヤコビ・ベルマン(HJB)方程式を導く.HJB方程式の古典的な一意可解性を示し,その定性的な解挙動をモデルパラメータの値にしたがい解析的に整理するとともに,現代的な水産資源管理手法の妥当性を検討する.
- ◎アユを魚食性鳥類から守るための最も経済的なテグス張り戦略 / ○八重樫 優太 (京都大学大学院農学研究科), 吉岡 秀和 (島根大学生物資源科学部), 宇波 耕一 (京都大学大学院農学研究科), 藤原 正幸 (京都大学大学院農学研究科) [概要]
春から夏にかけて河川中流域で成長するアユ稚魚の個体群を魚食性鳥類から守り,夏の漁解禁前まで存続させる方策として,漁業協同組合等による河川への“テグス張り”ある.本研究では,経済的に最も優れたテグス張り戦略を求めるための最適停止問題を定式化する.河川環境に応じたテグス張り導入時刻の支配方程式を導き,その存在や一意性についての数学解析結果を示す.また,数値計算を援用してテグス張り導入時刻に対する比較静学を行う.
▷ [一般講演] 数理モデル(2) [9月14日:15:00-16:20:2D](座長:斎藤 正也(統計数理研究所))
- 回復率の揺らぎを考慮した時間遅れを伴う感染症モデルの安定性解析 / ○石川 昌明 (山口大学大学院創成科学研究科) [概要]
近年,ジカ熱やデング熱などの感染症の流行抑制は解決すべき重要な社会問題になっている.マラリアのように媒介生物が媒介する感染症においては感染の時間遅れが生じ,また,環境の変化や個人差に起因して,モデルパラメータは平均値周りで不規則に揺らいでいると考えられる.そこで,本論文では特に,回復率の揺らぎを考慮した時間遅れを伴う確率感染症モデルを提案し,そのDisease-free平衡解の安定性を考察する.
- ◎拡散項と空間依存係数を持つ感染症モデルに対する Lyapunov 関数の構築 / ○國谷 紀良 (神戸大学大学院システム情報学研究科), 王 金良 (School of Mathematical Science, Heilongjiang University) [概要]
本研究では、拡散項と空間依存係数を持つ感染症モデルとして、SIR感染症モデルおよび細胞間感染を含むHIVモデルを構築し、それらの大域的な漸近安定性解析を行った。解析に必要となる Lyapunov 関数は、従来知られていなかったが、本研究では初めに離散化したモデルに対してグラフ理論的手法による Lyapunov 関数の構築を行い、離散化前のモデルの Lyapunov 関数の形状の示唆を得るという手法を採用した。
- ◎心肥大関連因子ネットワークを記述する常微分方程式のFeinberg理論を用いた解析 / ○小松 弘和 (近畿大学 工学部), 中島 弘之 (近畿大学 工学部), 伊藤 昭夫 (近畿大学 工学部) [概要]
Feinbergらの構築したChemical Reaction Network Theoryは,化学反応系を記述する常微分方程式を解析するための強力な手法であり,その核となる DZT(Deficiency Zero Theorem) は多くの系における正値平衡点の漸近安定性を保証する.
本講演では,心肥大関連因子ネットワークを記述する方程式にDZTを適用し,その平衡点の漸近安定性を証明した結果を報告する.
この系はDZTの条件である weak reversibility を持たないが,DZTが適用可能な部分系に分解することにより,平衡点の漸近安定性を証明する.
▷ [一般講演] 数理モデル(3) [9月14日:16:30-17:50:2D](座長:國谷 紀良(神戸大学))
- プラズマ物理学における高周波シースモデルの数理特性調査 / ○宮下 大 (住友重機械工業), 齊藤 宣一 (東京大学) [概要]
シミュレータ開発において事前に支配方程式の解の特性を把握しておくことは開発の手戻りを減らす上でも有用である。今回、高周波プラズマ源のシミュレーションに現れる2変数の非自励な連続非線形力学系で記述される高周波シースモデルの特性を調査した。自励系で近似し、相図法を利用することで解の特性を直感的に理解できるようなり、これまで不明であった解の発散の理由を明らかにし、また開発の手戻りを減らすことができた。
- 線形方程式と日本の河川の降雨流出解析との比較 / ○杉本 尚子 (九大 数理学府 数理学専攻 博士後期課程3年生) [概要]
土地利用の変化と流出との応答関係に着目すると,降水量と河川流量との関係になる.そこで降水量と河川流量データを使いimpulse response functionを計算しこの畳込み積分した結果と日本の河川で行った過去の降雨流出解析結果を比較したのでここに報告する.
- 2012/13年流行にもとづく風しん国内流行モデルの開発 / ○斎藤 正也 (統計数理研究所), 木下 諒 (統計数理研究所), 西浦 博 (北海道大学) [概要]
日本は風しんに対する集団免疫が確立する途上にあり,2012~13年に小規模な流行を経験している.この流行は大都市圏に集中しており(週例報告の最大は東京都で268例,大阪府で168例),30の都道府県では最大でも週例報告は10人以下であった.本講演では,確率的メタ・ポピュレーション・モデルによって2012/13年の流行が妥当なモデルパラメータのもとで再現できることを示す.
▷ [一般講演] 偏微分方程式(1) [9月13日:09:30-10:50:2D](座長:劉 雪峰(新潟大学))
- 偏微分方程式に対する陽的シングルステップ構造保存解法 / ○降籏 大介 (大阪大学) [概要]
構造保存解法は厳密解のもつ数学的性質の一部を厳密に再現する優れた解法であるが、非線形問題に対して通常得られる数値スキームは陰的かつ非線形であり、計算量が大きくなる問題点がある.
これまで提案されてきた多段線形化などの技法も、非線形性が強い偏微分方程式に対して実効性が低い.
そこで離散変分の概念を拡張することにより、単段かつ陽的な数値スキームを離散変分導関数法の概念で構成可能なことを示す.
- ◎非平坦時空におけるEinstein方程式の拘束伝播の解析 / ○浦川 遼介 (早稲田大学), 土屋 拓也 (早稲田大学), 米田 元 (早稲田大学) [概要]
Einstein方程式を数値的に解くときに,発展方程式に補正項として拘束条件を付加し拘束条件の破れが自己回復するような形式,adjusted systemが提案されている。従来の研究では,平坦な背景時空における摂動しか考慮されていなかったが,我々は非平坦な背景時空に対しても固有値解析を行い,背景時空に沿った拘束条件の破れを事前に予測できることを示した。
- ◎Einstein方程式の適切な離散式の構築について / ○土屋 拓也 (早稲田大学), 米田 元 (早稲田大学) [概要]
Einstein方程式は拘束条件付き発展方程式であり、拘束条件を満たすような離散方程式を構築することが困難である。本講演では、構造保存スキームを作る離散変分法を用い、さらに昨年度Maxwell方程式に対して行った拘束条件の時間発展方程式の離散式も組み込む手法を適用し、より精度の良い離散方程式を紹介する。また、変分を基とする離散手法とEinstein方程式は根本的な部分で相性が悪く、その解消法についても紹介する予定である。
▷ [一般講演] 偏微分方程式(2) [9月13日:11:00-12:20:2D](座長:降籏 大介(大阪大学))
- FitzHugh-Nagumoモデルにおける共存する解が接触する境界の挙動について / ○畑上 到 (金沢大学理工研究域) [概要]
代表的な反応拡散方程式であるFitzHugh-Nagumoモデルを取り上げ,共存する複数の解が空間的に接触している界面の構造を数値的に解析した.特に本研究では,静的な(定常的な)解と動的に振動する解との間に生成する境界について考察する.この境界が生成する過程での静的な解側の同期現象や共存する解の安定度との関連についての結果を報告する.また,このような界面を効率的に生成させるために提案した初期条件についても報告する.
- メッシュレス法を用いた内部・外部混合境界値問題の数値解法 / ○齋藤 歩 (山形大学), 高山 彰優 (山形大学), 神谷 淳 (山形大学) [概要]
FEMやBEMのように要素分割を必要としないため,近年,新たな数値解法としてメッシュレス法が注目されている.本講演では,メッシュレス法を用いた内部・外部混合境界値問題の数値解法を提案し,同法の性能を数値的に評価した結果を示す.
- 動径基底関数による連続時間非線形フィルターの近似 / ○中野 張 (東京工業大学) [概要]
システムが一般の拡散過程で与えられる場合のフィルタリング問題において,動径基底関数を用いたメッシュフリー法によるZakai方程式および最適フィルターの近似を提案し,理論的な収束について報告する.
- 4探針法による半導体材料抵抗率の高精度な測定について / ○劉 雪峰 (新潟大学), 中本 昌雄 (ナプソン株式会社) [概要]
4探針法によるウェハーなどの半導体材料の抵抗率を測定するとき、測定対象(=領域)の上に定義されるポアソン方程式の解の計算が必要である。
該当微分方程式のモデルにはDiracの超関数が現れるので、解の計算は困難である。特に、従来の測定方法ではウェハーのエッジ付近の測定誤差が大きいという問題がある。
本研究は有限要素法を利用することで、ポアソン方程式の解の高精度かつ効率的計算手法を提案した。
▷ [一般講演] 偏微分方程式(3)/[一般講演] 統計科学 [9月13日:13:30-14:50:2D](座長:齋藤 歩(山形大学))
- Error analysis of Lagrange interpolation on tetrahedrons / ○小林 健太 (一橋大学), 土屋 卓也 (愛媛大学) [概要]
四面体上の新しいタイプのLagrange補間誤差評価について報告する。
この補間誤差評価は、射影外接半径という幾何学的な量に基づいており、補間誤差が悪化しないような四面体の潰れ方にも対応した誤差評価になっている。
- ストークス方程式の直交選点有限要素法による定式化と境界条件の取り方 / ○大久保 孝樹 (函館高専 社会基盤工学科) [概要]
直交選点有限要素法(OCFEM)において、2次元ストークス方程式を解く際に、水路入口部の圧力勾配がゼロという条件を入れた場合、水路入口部での圧力の変化が強制的に変えられるので、OCFEMでは振動する圧力分布になる傾向がある。OCFEMに合う、入口部での圧力の2階の微分がゼロ(圧力勾配が変化しない)という条件は、数学物理的にも整合性が取れるものと考えられ、良い結果が得られた。
- ルジャンドル陪関数の変形と応用11 / ○田川 昭夫 (なし) [概要]
ルジャンドル陪関数を変形すると、
Rnm(cosθ)*(sinθ)^mの形になる。
Rnmの隣接項間の式が見つかり応用して、
定常流のストークス近似式が解ける。
等速運動をする球体の流れを解くと、
ストークスのパラドックスが級数解として現れるが、
δ/δx{Rnm}=Rn-1.m+1を応用して、
係数が漸化式の形で求められる。
抗力係数は、24/Re+28/25。
- ジカウイルスの国際伝播に関する予測モデルの開発 / ○西浦 博 (北海道大学), Nah Kyeongah (北海道大学) [概要]
ジカウイルスは妊娠中の感染と小頭症との因果関係が最近に強く示唆されたことを端緒に注目を集めている.本研究では,世界各国のジカ熱の輸入リスクと国内伝播のリスクを推定する新しい統計モデルを開発し,推定結果を発表した。ヒトの国際移動に関するネットワークデータと媒介蚊およびデング熱・チクングニヤ熱の情報を用いて生存解析モデルを定量可能にし,2016年1月までの観察データを分析した.その結果,ほとんどの国で,時間が経過するにつれてジカ熱を輸入する可能性が十分にあると予測された。また,モデル比較により,これまでにデングウイルスやチクングニアウイルスの国内伝播が認められた国においてジカ熱の国内伝播リスクが高いことが明らかになった。提案したモデルはジカ熱の国際的流行拡大に関するリスクアセスメントを実施する上で重要な科学的根拠を与える。日本において2016年中にジカ熱の国内伝播を認めるリスクは16.6%と推定された。同リスクはメキシコで48.8%,台湾で36.7%など,デング熱やチクングニア熱の流行を認めた熱帯・亜熱帯地域でより高く,一方,温帯では英国で6.7%,オランダで5.3%など日本よりも低い国もあった。
▷ [一般講演] 離散システム [9月12日:16:30-17:50:2B](座長:南畑 淳史(早稲田大学))
- ◎Min-Plus代数における複数の固有値を持つ行列のグラフ構造 / ○渡辺 扇之介 (京都府立大学生命環境学部), 保田 愛斗 (京都府立大学生命環境学部), 岩崎 雅史 (京都府立大学生命環境学部), 渡邊 芳秀 (同志社大学理工学部) [概要]
Min-Plus代数とは,実数に無限大を加えた集合に2つの二項演算和と積を,それぞれminと+で定義した代数である.
このMin-Plus代数における行列の最小固有値は,その行列を重み付き隣接行列とするグラフ上のネットワークにおける閉路の最小平均重みと一致することが知られている.
本講演では,Min-Plus行列の最小固有値以外の固有値とグラフとの関係について議論する.
- ◎保存密度によるECAの分類 / ○茶山 斉範 (同志社大学理工学部), 渡辺 扇之介 (京都府立大学生命環境学部), 渡邊 芳英 (同志社大学理工学部) [概要]
複数の格子状のセルの中に状態量を割り当て、局所的な規則によって時間発展させる数理モデルをCellular Automata (CA)という。
特に、状態量を0、1として、自身とその隣り合ったセル(3近傍)の状態量で規則が決まるCAをElementary CA (ECA)という。
本講演ではECAの時間発展規則を有理係数の多項式として表現する。
さらに、この多項式表現を用いて、様々な保存密度で決まる保存量を持つECAを列挙する。
- ◎単純 b-マッチングの Dulmage-Mendelsohn 分解 / ○喜多 奈々緒 (国立情報学研究所) [概要]
マッチング理論においては総称して標準分解と呼ばれるいくつかの分解型構造定理が強力な道具となるが,古典的な Dulmage-Mendelsoh 分解とは 2 部グラフを対象する標準分解のひとつであり,与えられた 2 部グラフが持つ標準的な束構造を通して全ての最大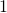 -マッチングとその双対最適解である最小点被覆の族の構造を記述する.これはグラフ理論的文脈のみならず,大規模疎行列による連立方程式の効率的解法など行列計算の分野への応用が報告されている他,基本分割理論の原型を与えるなど劣モジュラ関数論への貢献が知られている.一方,
-マッチングとその双対最適解である最小点被覆の族の構造を記述する.これはグラフ理論的文脈のみならず,大規模疎行列による連立方程式の効率的解法など行列計算の分野への応用が報告されている他,基本分割理論の原型を与えるなど劣モジュラ関数論への貢献が知られている.一方,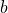 -マッチングもまた古典的な概念でありこれは
-マッチングもまた古典的な概念でありこれは 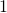 -マッチングの代表的な一般化である.本研究では Dulmage-Mendelsohn 分解を
-マッチングの代表的な一般化である.本研究では Dulmage-Mendelsohn 分解を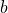 -マッチングを対象にするものへと一般化を与え,古典的な成果と同様,2 部グラフの半順序構造の抽出ひいて最大
-マッチングを対象にするものへと一般化を与え,古典的な成果と同様,2 部グラフの半順序構造の抽出ひいて最大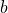 -マッチングおよび双対最適解の構造を記述する.
-マッチングおよび双対最適解の構造を記述する.
- Fitzhugh-Nagumo 型反応拡散系への超離散法の適用 / 大森 祥輔 (早稲田大学 理工学術院), ○山崎 義弘 (早稲田大学 理工学術院) [概要]
散逸系のパターン形成現象を表現する具体的な微分方程式系として、Fitzhugh-Nagumo 型の反応拡散系に着目し、超離散法を適用して得られた超離散方程式からセルオートマトンのルールを抽出した。そして、超離散双安定性、および、興奮性におけるパルス解の挙動をセルオートマトンとして表現した。本発表では、導出の過程を説明し、得られたセルオートマトンによる時空パターンについて紹介する。
▷ [一般講演] 流体計算 [9月13日:13:30-14:50:2B](座長:関根 晃太(早稲田大学))
- 符号付き距離関数の離散時間毎再構築による2流体有限要素計算 / ○鈴木 厚 (大阪大学 サイバーメディアセンター), 大森 克史 (富山大学 人間発達科学部) [概要]
符号付き距離関数によるレベルセット法では2流体問題は異なる流速, 粘性を特性関数で表すことにより, 境界を陽に記述せず単一の方程式で解く. レベルセットは流速場により移流されるが誤差の累積を防ぐため, 双曲型偏微分方程式による再初期化手法が用いられることが多い. しかしながら, 要素毎での零等高線を扱うことで符号付き距離関数を有限要素から再構築でき, 表面張力の線積分は部分積分により曲率の微分無しに計算できることを示す.
- 移流輸送計算の高精度化に関する研究 / ○坪郷 浩一 (放送大学) [概要]
本研究では,特性曲線法に基づく高次精度計算スキームの開発を行った.この計算スキームを5次精度6-point scheme と名付ける.Taylor級数展開による打ち切り誤差は,5次精度を満足するが,この計算スキームは保存形式ではないためTVD条件を満足していない.そこで,5次精度6-point scheme を保存形式へ変換し,flux limiter とdiscriminator を適用してTVD条件を満足させる.この変換した計算スキームを5次精度保存形式6-point scheme と名付ける.提案する計算スキームは,1次元および2次元移流問題のモデルケースにおいて,従来の高精度かつ高解像度計算スキームと言われる離散化手法と比べて厳密解に近い値が得られ,さらに,多次元問題にも容易に適用できる.また,この計算スキームにおける境界近傍処理は,境界外濃度値を境界上の値と同値にする簡便な方法で精度の良い結果が得られたので,報告する.
- Mathematical models of a turbulent atomized liquid jet through conservation of mass flux and power / ○Franco Medrano Fermin (九大院数理), 福本 康秀 (九大MI研) [概要]
We propose two-phase-fluid mathematical models for a turbulent full-cone high-speed atomizing liquid jet that describe its dynamics in a simple but comprehensive manner with the apex angle of the cone being the main disposable parameter. The basic assumptions are that (i) the jet is statistically stationary and that (ii) it can be approximated by a mixture of a liquid and a gas with its phases in dynamic equilibrium. To derive the model, we impose partial conservation of the liquid mass and total power fluxes introducing mass and energy loss factors again as disposable as parameters. Our model equations admit semi-analytical and numerical solutions for the composite density and velocity of the two-phase fluid, both as functions of the distance from the nozzle, from which the dynamic pressure and gas entrainment rate coefficient are calculated. Moreover, we show that the predictions of our models compare well with experimental data.
- Lennard-Jones流体の気泡核生成に関する分子動力学解析 / ○釜野 竜一 (早稲田大学大学院 基幹理工学研究科 機械科学専攻), 菅原 匠 (早稲田大学 基幹理工学部 機械科学・航空学科), 吉村 浩明 (早稲田大学 基幹理工学部 機械科学・航空学科) [概要]
本研究では,Lennard-Jones流体を用いた分子動力学法により,ナノスケールの気泡核の自然生成を再現し,気泡核生成前後の温度,密度,圧力,気泡核半径等のパラメータに注目することで気泡核生成に関する数値解析を行う.また,流体中に不純物が混在した場合,それが気泡核生成に及ぼす影響についても調査する.さらに,系の状態を相図における熱力学的安定限界を表すスピノーダル曲線と比較し,系の安定性に関する考察を行う.
▷ [研究部会OS] ウェーブレット(1) [9月14日:09:30-10:50:2D](座長:[前半]藤田 景子(富山大学),[後半]藤ノ木 健介(東海大学))
- ◎壁からの信号とそれに埋もれた単信号へのブラインド再構成 / ○佐々木 裕文 (早稲田大学), 佐々木 文夫 (東京理科大学), 山田 道夫 (京都大学) [概要]
音のような信号解析のアプローチとしてブラインド信号源分離があり,その応用としてブラインド再構成がある.ブラインド再構成は信号分離のみならず観測信号から様々な情報を解析,再構成することを目的としている.今回のモデルとして,壁からの信号ともう一つの信号を考え,壁からの信号は非常に大きなものとする.このとき観測信号から,信号源,信号と壁の位置を求める手法を提案し,数値実験により本手法の有用性を示す.
- ウェーブレット解析に基づいた画像分離について / ○守本 晃 (大阪教育大学), 芦野 隆一 (大阪教育大学), 萬代 武史 (大阪電気通信大学) [概要]
平行移動をともなった画像の重ね合わせを複数個観測し,
観測画像から元画像を推定する画像分離問題にたいして,
ウェーブレット解析に基づいた解法について考察する.
- [40分講演] ◎ウェーブレット変換に基づくディストーションサウンドの特徴量抽出 / ○鈴木 俊夫 (筑波大学), 善甫 啓一 (筑波大学), 木下 保 (筑波大学) [概要]
ディストーションサウンドが用いられている音楽の耳コピの精度は,個人の能力や経験に大きく依存する.しかし,ディストーションフィルタはクリッピングを含む非線形変換であるため,Fourier変換を用いた解析は難しい.今回我々はウェーブレット変換を用いたディストーションサウンドの特徴量抽出に関する手法を提案する.さらにディストーションサウンドのレベルを比較する被験者実験を行い,提案手法についての妥当性も得られたので報告する.
▷ [研究部会OS] ウェーブレット(2) [9月14日:11:00-12:20:2D](座長:[前半]鈴木 俊夫(筑波大学),[後半]守本 晃(大阪教育大学))
- 聴性脳幹反応による聴力閾値推定に用いるウェーブレット解析について / ○井川 信子 (流通経済大学), 守本 晃 (大阪教育大学), 芦野 隆一 (大阪教育大学) [概要]
音刺激音圧を徐々に下げ聴こえを確認し聴力閾値を求めてオージオグラムを描画する自覚聴力検査が一般的である.一方,この検査が難しい場合,聴性脳幹反応という誘発脳波を用いて聴力閾値を推定する方法がある.振幅が小さい聴力閾値における波形にウェーブレット解析を用いることで聴力閾値を推定する方法について考察する.
- 瞬間振幅に関する不等式について / ○萬代 武史 (大阪電気通信大学) [概要]
与えられた実信号(関数)に対して,そのヒルベルト変換を虚部に持つ複素信号は,解析信号と呼ばれ正の周波数成分のみを持つ.解析信号の絶対値は瞬間振幅と呼ばれ,多くの場合,元の信号の大まかな変動を表すエンヴェロープのようなものになるが,そうでない場合もある.元の信号の周波数帯が狭い場合には,瞬間振幅が緩やかな変化をすることを意味するある不等式を証明できたので,それを報告する.
- [40分講演] ◎非分離型半重複双直交ウェーブレット分解 / ○藤ノ木 健介 (東海大学), 芦澤 恵太 (舞鶴工業高等専門学校) [概要]
画像の効率的な方向性解析のための新たな変換方法を提案する.非分離型2次元離散ウェーブレット変換において,半重複ポリフェーズ分解により制限付き冗長性を導入することで,方位選択性を従来の3方向から最大12方向まで拡張した双直交ウェーブレット分解が実現できることを示す.画像に対する数値実験結果によってその優位性を示す.
▷ [研究部会OS] 応用カオス(1) [9月12日:13:30-14:50:3E](座長:後藤 振一郎(京都大学))
- 戻り光半導体レーザーを用いたリザーバーコンピューティングに関する数値的研究 / ○島田 航行 (金沢大学), 砂田 哲 (金沢大学), 新山 友暁 (金沢大学) [概要]
本研究では半導体レーザー素子を用いたリザーバコンピューティングについて,時系列予測シミュレーションの作成,および予測精度の評価を行った.またリザーバーを構成する仮想ノードの数や入力信号マスク等のパラメータが予測性能に与える影響についても考察を行ったのでその結果について報告する.
- レーザーカオスと金属V溝を用いた高効率テラヘルツ分光装置 / ○桒島 史欣 (福井工大), 白尾 拓也 (福井工大), 岩尾 憲幸 (福井工大), 赤峰 佑介 (福井工大), 大井 真夏 (福井工大), 坂上 直哉 (福井工大), 白崎 拓郎 (福井工大), 合田 汐里 (福井工大), 谷 正彦 (福井大), 栗原 一嘉 (福井大), 山本 晃司 (福井大), 森川 治 (海上保安大学校), 長島 健 (摂南大学), 中島 誠 (大阪大) [概要]
レーザーカオスによるTHz波の安定発生および広帯域化とこれまでTHz領域では発生しないといわれてきた、金属V溝による超集束効果による検出感度の向上について報告する。
- ◎シンプレクティック写像における超拡散と密度関数の振る舞い / ○大久保 健一 (京大情報), 梅野 健 (京大情報) [概要]
講演者は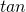 関数を用いたシンプレクティック写像を考案し, 解析を行ってきた. この写像において, あるパラメータ領域で,
超拡散が発生することが数値計算によってわかった. このとき, 角変数に対する不変密度が一様分布であることが解析的に
わかっており, 時刻
関数を用いたシンプレクティック写像を考案し, 解析を行ってきた. この写像において, あるパラメータ領域で,
超拡散が発生することが数値計算によってわかった. このとき, 角変数に対する不変密度が一様分布であることが解析的に
わかっており, 時刻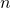 での作用変数がコーシー分布に従う
での作用変数がコーシー分布に従う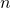 個の確率変数の和で表せる. このことから,
確率密度関数の時間発展について述べる.
個の確率変数の和で表せる. このことから,
確率密度関数の時間発展について述べる.
- カオス尺度からリアプノフ指数への変換の可能性 / ○井上 啓 (山陽小野田市立山口東京理科大学) [概要]
カオス尺度は、情報理論の観点から導入されたカオスを定量化する指標である。本発表では、一般化シフト写像を通して得られるカオス尺度からリアプノフ指数への変換方法について、ロジスティック写像への適用を試みる。
▷ [研究部会OS] 応用カオス(2) [9月12日:15:00-16:20:3E](座長:山口 明宏(福岡工業大学))
- 心拍間隔データのカオス尺度と自律神経活動の関連について / ○真尾 朋行 (東芝情報システム株式会社), 奥富 秀俊 (東芝情報システム株式会社) [概要]
これまで我々は、心拍間隔データからカオス尺度を計算し運転中に起こる眠気との関連を示唆する報告を行ってきた。
しかし、運転中の状態は副交感神経・交感神経ともに明らかに優位な状態とはいえないため、両者の差がより顕著であると思われる座位安静と起立負荷状態において同実験を行い、カオス尺度と自律神経活動との関連を調査した。
- 心拍間隔に基づく自律神経の活動指標に関する考察 / ○奥富 秀俊 (東芝情報システム), 真尾 朋行 (東芝情報システム) [概要]
心拍間隔データに基づき自律神経の活動状態を知るための指標として,主としてSDNN,SDSD, pNN50, LF, HF, 等が使われる.これらの指標と,著者らが扱うカオス尺度との関係性について考察する.
- Superefficientなモンテカルロ計算アルゴリズムとその最適化について / ○梅野 健 (京都大学情報学/東京大学物性研) [概要]
混合性を持つカオス系列で, 滑らかさがない至るところ微分不可能な被積分関数に対しても誤差分散が通常の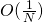 から
から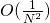 となるSuperefficientモンテカルロ計算法(SMC)について、存在定理と最適アルゴリズムの構成を示す。存在定理は、
となるSuperefficientモンテカルロ計算法(SMC)について、存在定理と最適アルゴリズムの構成を示す。存在定理は、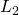 上の任意の被積分関数に対してSMCが可能であることを意味し、最適アルゴリズムは、SMC条件を与える部分ヒルベルト空間へのルベーグスペクトル
上の任意の被積分関数に対してSMCが可能であることを意味し、最適アルゴリズムは、SMC条件を与える部分ヒルベルト空間へのルベーグスペクトル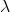 理論から構成される射影演算子
理論から構成される射影演算子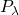 で与える。
で与える。
- 電気回路系の接触幾何学的および情報幾何学的記述 / ○後藤 振一郎 (京都大学) [概要]
RLC回路等の電気回路に起因する力学系の接触幾何学的及び情報幾何学的記述を行う。この記述法により、構成方程式 (例えば、RC回路では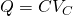 、ここで
、ここで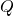 はコンデンサに蓄えられる電荷、
はコンデンサに蓄えられる電荷、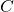 は静電容量、
は静電容量、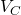 はコンデンサ間の電圧) や電磁エネルギ関係式 (RC回路では
はコンデンサ間の電圧) や電磁エネルギ関係式 (RC回路では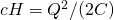 ) を拘束条件と見做した接触多様体上の力学系になることを示す。特に電圧源無しのRLC 直列回路の力学系は、ルジャンドル部分多様体や情報幾何学で用いられる双対平坦空間上での力学系であることも示す。
) を拘束条件と見做した接触多様体上の力学系になることを示す。特に電圧源無しのRLC 直列回路の力学系は、ルジャンドル部分多様体や情報幾何学で用いられる双対平坦空間上での力学系であることも示す。
▷ [研究部会OS] 応用カオス(3)(〜18:10) [9月12日:16:30-18:10:3E](座長:奥富 秀俊(東芝情報システム))
- 2冪剰余環上一筆書き多項式の周期を延長する結合方法について / ○岩崎 淳, 梅野 健 [概要]
2冪剰余環上置換多項式のうち,多項式のなす軌道の周期が最大となる(一本の軌道が2冪剰余環をくまなくめぐる)多項式を(2冪剰余環上)一筆書き多項式と呼ぶ.一筆書き多項式の周期は確かに長いが,時間発展する単一の変数のビット長に制限されてしまう.本発表では,一筆書き多項式を複数組み合わせ複数の変数を時間発展させることを考え,組み合わせることで周期を延ばす方法を紹介する.
- ◎CDMA拡散符号の改善のためのSNR式の再表現 / ○津田 宏史 (京都大学情報学研究科), 梅野 健 (京都大学情報学研究科) [概要]
CDMA拡散符号の良し悪しはSNR式という指標によって主に評価される。PursleyによってSNRを評価する式が構成されたが、その式は複雑であり、SNRを最大化する問題を考えたときには扱いづらい。そこで本発表では拡散符号の基底としてWeyl拡散符号を選ぶことで、Pursleyとは異なる方法でSNR式を導出する。この結果、非線形計画問題としてSNRの最大化の問題を構成することができた。
- 整数上のロジスティック写像におけるコントロールパラメータとビット毎の出現確率の関係 / ○村岡 英之 (九州工業大学), 荒木 俊輔 (九州工業大学), 宮崎 武 (北九州市立大学), 上原 聡 (北九州市立大学), 硴崎 賢一 (九州工業大学) [概要]
本稿では,擬似乱数生成器として利用を想定してビット抽出位置を定めるために,整数上のロジスティック写像により生成される値において,これまで議論されていなかった4以外のコントロールパラメータとビット毎の0/1の出現確率の関係について議論する.特に,コントロールパラメータの下位のいくつかのビットによって,出力値の下位ビットの0/1の出現確率を4つに分類できることを示す.
- 素体上のロジスティック写像による系列の平均周期・リンク長期待値 / ○宮﨑 武 (北九州市立大学), 荒木 俊輔 (九州工業大学), 上原 聡 (北九州市立大学), 野上 保之 (岡山大学) [概要]
繰り返し写像による擬似乱数生成器の設計のため,素体上のロジスティック写像による生成系列の性質を調査している.系列のループ・リンク部分の写像回数である周期・リンク長は,整数上のロジスティック写像での周期・リンク長近似値を求めたモデルを下敷きに算出することができる.本稿では,これらの周期・リンク長について期待値を算出し,実際の生成系列から得られた実測値と比較する.
- カオス真軌道から構成した相関系列に対するNIST乱数検定の判定結果の解析 / ○山口 明宏 (福岡工業大学), 斉藤 朝輝 (公立はこだて未来大学) [概要]
擬似乱数系列の乱数性の判定法としてNIST乱数検定(SP800-22)がよく知られている.NIST乱数検定では,15種類188項目の検定が適用されるが,各検定項目間の相関構造や独立性の解析についての研究は少ない.本研究では,ベルヌーイシフト写像のカオス真軌道から生成した擬似乱数系列から構成した相関を有する系列についてNIST乱数検定を適用した結果を報告する.
▷ [研究部会OS] 応用可積分系(1) [9月13日:09:30-10:50:1A](座長:由良 文孝(はこだて未来大学))
- 離散ハングリー戸田方程式の連続類似 / ○西山 雄祐 (同志社大学), 近藤 弘一 (同志社大学) [概要]
離散ハングリー戸田方程式は,有限の離散力学系であり,離散可積分系の一つと考えられている.しかしながら,その連続類似としての微分方程式は導出されていない.本発表では,まず離散ハングリー・ロトカ・ボルテラ方程式に関する一般解,ラックス対,ラックス表示を求める.次に,ベックルンド変換により非自励な離散ハングリー戸田方程式を導出する.最後に連続極限をとり,連続なハングリー戸田方程式とその一般解を導出する.
- 2次元離散戸田方程式の擬可積分拡張 / ○神谷 亮 (東大数理), 神吉 雅崇 (関西大システム理工), 時弘 哲治 (東大数理), 間瀬 崇史 (東大数理) [概要]
離散2次元戸田格子方程式に4つのパラメータを導入したある3次元格子方程式について議論する。
その方程式は、離散2次元戸田格子方程式の擬可積分な拡張である。すなわち、特殊な場合として離散2次元戸田格子方程式を含み、一般の場合には次数が指数的に増大するがco-primeness条件を満足する(特異点閉じ込めテストに通る)。
- クラスター代数とセルオートマトン / ○野邊 厚 (千葉大学), 間田 潤 (日本大学) [概要]
ランク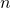 のクラスター代数に対応する
のクラスター代数に対応する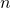 正則木上のクラスターパターンをうまく選ぶと,クラスター代数の変異からシステムサイズ
正則木上のクラスターパターンをうまく選ぶと,クラスター代数の変異からシステムサイズ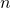 のセルオートマトンを導出することが可能である.本講演では,
のセルオートマトンを導出することが可能である.本講演では,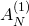 型クラスター代数を用いたセルオートマトンの構成について議論する.
型クラスター代数を用いたセルオートマトンの構成について議論する.
- ◎コーシー・ビネの公式の超離散対応物 / ○長井 秀友 (東海大学理学部) [概要]
超離散パーマネントは行列式の超離散対応物としてみることができ,事実いくつかの超離散ソリトン方程式の解は,この超離散パーマネントを用いて表すことが知られている.本講演ではコーシー・ビネの公式に類似した等式を超離散パーマネントが持つことを紹介する.さらにこの等式といくつかの関係式をうまく利用することで,超離散KP方程式の超離散パーマネント解が与えられることを示す.
▷ [研究部会OS] 応用可積分系(2) [9月13日:11:00-12:20:1A](座長:長井 秀友(東海大学))
- 束方程式の解の挙動について / ○安藤 卓哉 (早稲田大学), 高橋 大輔 (早稲田大学) [概要]
共役元を持つ分配束上で,束の演算を用いた方程式とその解を考える.
その特殊化として,Boole束の場合はこのような方程式によってECAを
表現できる.また実数体上のmax, minの方程式もこの枠組みに含まれる
場合がある.講演では半順序集合上の束の場合も考慮しながら,
それぞれの束における解の振る舞いの相似と相異について議論する.
- 粒子セルオートマトンの3次元基本図について / ○高澤 俊介 (早稲田大学), 高橋 大輔 (早稲田大学) [概要]
粒子セルオートマトンでは,保存量である粒子密度を横軸に,平均流束を縦軸にとった2次元の基本図が標準的に用いられる.ところが,2つの独立な保存量を同時に有する系で,それら2つを横軸に用いた3次元の基本図によって相転移現象が明快にわかる例が見つかった.そこで,さまざまな粒子セルオートマトンでこのような3次元基本図を持つような例を探索し,解の振る舞いについて論じる.
- Persymmetric Jacobi 行列に付随する直交多項式の構成方法 / ○辻本 諭 (京都大学), Genest Vincent (マサチューセッツ工科大学), Vinet Luc (モントリオール大学), Zhedanov Alexei (ドネツク物理工科研究所) [概要]
はじめに、Persymmetric Jacobi 行列の一般的性質について議論する。その後、付随する直交多項式を導入し、与えられたスペクトル列から対応するPersymmetric Jacobi 行列を再構成する手続きについて考察する。
- 離散例外型直交多項式から導かれる出生死滅過程の拡張 / ○三木 啓司 (同志社大学), 齊藤 昭洋 (同志社大学) [概要]
本講演では,例外型直交多項式と呼ばれるSturm-Liouville作用素の新しい多項式固有関数の離散類似について,漸化式などの性質を述べる.また,得られた多項式が離散古典直交多項式の一種の拡張になるという事実に基づき,古典直交多項式に付随する出生死滅過程の拡張を与える.
▷ [研究部会OS] 応用可積分系(3) [9月13日:13:30-14:50:1A](座長:神吉 雅崇(関西大学))
- Modified short pulse方程式の可積分自己適合移動格子スキーム / ○徐 俊庭 (早稲田大学基幹理工学研究科), 丸野 健一 (早稲田大学理工学術院), Feng Bao-Feng (University of Texas Rio Grande Valley), 太田 泰広 (神戸大学理学研究科) [概要]
Feng-Maruno-Ohtaは、short pulse方程式の可積分自己適合移動格子スキームを提案し、それが数値計算法として有効であることを示した。これまで様々な方程式で自己適合移動格子スキームは構成されているが、Hunter-Saxton方程式などのカスプ型のソリトン解を持つ方程式に対しては数値計算が困難であった。本講演では、カスプ型ソリトン解を持つmodified short pulse方程式の可積分自己適合移動格子スキームの構成とそれを用いた数値計算について報告する。
- MKdV流と弾性曲線の統計力学 / ○松谷 茂樹 (佐世保工業高等専門学校), Previato Emma (Boston University) [概要]
平面曲線の変形において,等長変形のみならず,弾性エネルギーの不変性を要請し,系の自明な変形を加味すると,自然に変形KdV階層が現れる.本報告ではそのことを示す (arXiv:1511.08658).
- 棒のたわみの周期境界値問題とソボレフ不等式の最良定数 / ○山岸 弘幸 (都立産技高専), 永井 敦 (日大生産工), 亀高 惟倫 (阪大) [概要]
バネ定数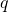 の弾性基盤上におかれ,張力
の弾性基盤上におかれ,張力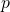 をかけた棒のたわみの周期境界値問題を考えた.
をかけた棒のたわみの周期境界値問題を考えた.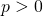 なら張力,
なら張力, なら圧力を表す.
なら圧力を表す.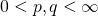 または
または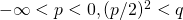 を想定し,それぞれのグリーン関数を求めた.対応するソボレフ不等式は,棒のたわみの最大幅を棒のポテンシャルエネルギーの定数倍で評価する不等式となる.定数倍のうち,最も小さい最良定数がわかると,棒のたわみの最大幅を正確に見積もることができる.最良定数はグリーン関数の対角成分で与えられ,等号を達成する関数もグリーン関数で記述できる.
を想定し,それぞれのグリーン関数を求めた.対応するソボレフ不等式は,棒のたわみの最大幅を棒のポテンシャルエネルギーの定数倍で評価する不等式となる.定数倍のうち,最も小さい最良定数がわかると,棒のたわみの最大幅を正確に見積もることができる.最良定数はグリーン関数の対角成分で与えられ,等号を達成する関数もグリーン関数で記述できる.
- ◎最適速度模型 / ○室 暁生 (東京大学大学院工学系研究科航空宇宙工学専攻), 西成 活裕 (東京大学 先端科学技術研究センター 教授) [概要]
自動車の追従挙動を表すモデルとしてOptimal Velocity Model (OVM)が知られている。OVMは密度流量の関係などが詳しく研究されているが、これを製造過程における物流といった輸送システムに応用することが考えられる。ただし、応用を簡単にするための工夫として、最適速度関数を階段状の関数にし、さらに、加速度を最適速度と実際の速度の差に比例する形ではなく定数とした。このシステムの挙動を流量を中心に説明する。
▷ [研究部会OS] 折紙工学(1)(〜12:40) [9月12日:11:00-12:40:1A](座長:石田 祥子(明治大学))
- 対数螺旋格子の上の円板充填 / ○山岸 義和 (龍谷大学), 須志田 隆道 (北海道大学) [概要]
螺旋葉序に関する van Iterson の円板充填モデル(1907年)における半径が、平面の距離関数の公理を満たすことを示す。対数螺旋格子のボロノイタイリングの分岐が、この距離関数の方程式で記述される。円板充填の斜列係数は、同じ格子によるボロノイタイリングの斜列係数でもある。これにより、円板充填の van Iterson の分岐図が、ボロノイタイリングの分岐図の双対グラフであることが示される。
- 折り畳み可能な球面近似と蛇腹折り / ○奈良 知惠 (明治大学 MIMS) [概要]
曲面を可展面で近似するとき、その展開図と平坦折り畳み形状が重要になる. さらに,曲面状態から平坦折り畳み状態までの「動き」(すなわち,連続的折り畳み)が特定できると応用面でも好都合である. ここでは,球面を近似する長方形の蛇腹折りと糊付けの設計(2通り)について最初に述べ,次に,より一般的な曲面としてヘルメットのカバーに応用された形状を例に挙げて,連続的折り畳みの方法を紹介する.
- ◎A Computational Design Method for Tucking Axisymmetric 3D Origami Consisting of Triangle Facets / ○Zhao Yan (University of Tsukuba), Kanamori Yoshihiro (University of Tsukuba), Mitani Jun (University of Tsukuba) [概要]
The family of axisymmetric three-dimension (3D) origami consisting of triangle facets has one degree of freedom when it is developed or flat-folded along arc-direction. Such 3D origami can be potentially used to fold an origami dome. In this paper, we propose a design method to edit such kind of 3D origami directly. During the editing process, the crease pattern is updated. Blank spaces (unfolded areas) could emerge in the crease pattern. We then calculate the shape of flaps outside or tucks inside (that are folded from the blank spaces) to achieve the resultant 3D origami. Using our system, we construct several new 3D origami pieces with tucks inside or flaps outside. Finally, on the application side, we make a load-bearing experiment on a stool shape-like origami with tuck inside to show the potential usage of our origami piece.
- Design and Fabrication of Aluminum Honeycomb Cores Based on Origami Technology / 王 麗君 (東京大学生産技術研究所), ○斉藤 一哉 (東京大学生産技術研究所), 五島 庸 (城山工業株式会社), 岡部 洋二 (東京大学生産技術研究所) [概要]
In this study, the hexagonal honeycomb cores were designed and developed by using the origami technology, and the aluminum honeycomb structure materials were fabricated by press and folding processes. The mechanical properties of the honeycomb cores were investigated, and the results showed excellent mechanical properties. It offers a good method to develop a better structural material in different applications such as automotive industries, even aviation and aerospace fields.
- ハニカムパターン設計のための切紙モデル / ロメロ ジュリアン (明治大学), ○ディアゴ ルイス (明治大学), 奈良 知惠 (明治大学), 萩原 一郎 (明治大学) [概要]
紙を折り,糊付けまでできる,自ら命名したNorigamiロボットを開発した.既に蛇腹折りベースの袋の自動化をこのNorigamiロボットで成功させた例は米国機械学会ロボットコンテストでファイナリストに選ばれ,これから最終審査に向かうところである.本報告では,新たに折紙ハニカムを自動的に折り糊付けするアルゴリズムについて報告する.
▷ [研究部会OS] 折紙工学(2) [9月12日:13:30-14:50:1A](座長:斉藤 一哉(東京大学))
- 斜め荷重を考慮した展開可能なコア構造に関する検討 / ○石田 祥子 (明治大学理工学部機械工学科) [概要]
本講演では,低剛性な展開収縮構造と高剛性なコア構造を組み合わせた,展開収縮可能なコア構造について述べる.本構造は高さ方向に展開収縮部とコア部が交互に配置されており,コア上面に垂直荷重を受けると展開収縮部が一様に折りたたまれコア構造となる.また,コア上面に斜め荷重を受けると,荷重につりあうように展開収縮部が局所的に伸縮できるため,構造は柔軟に曲げ変形を起こし,荷重を支持することができる.
- 折り畳みモデルの圧潰シミュレーション / ○阿部 綾 (明治大学先端数理科学インスティテュート), 楊 陽 (明治大学先端数理科学研究科), 王 麗君 (東京大学生産技術研究所), 奈良 知惠 (明治大学先端数理科学インスティテュート), 安達 悠子 (明治大学先端数理科学インスティテュート), 萩原 一郎 (明治大学先端数理科学インスティテュート) [概要]
折紙工学に基づいて、飲料容器を想定したモデルを構築し、圧潰時の挙動を検討した。いくつかの設計パラメータに対する最適設計を行い、荷重が軸方向に平行でない場合についても充分に潰れるか検討した。
- コンパクトな折り紙へルメットの衝撃特性 / ○楊 陽 (明治大学), 奈良 知惠 (明治大学), 萩原 一郎 (明治大学) [概要]
地震や自転車事故の際,安全を守る最も身近なものの一つに安全ヘルメットや安全帽子がある。 特にヘルメットの場合,教室内に置くと通路が狭くなり,ロッカーに入らないという事態も生じている。これを解決すべく折り畳みのヘルメットが期待される。コンパクト収納に優れと保護規格を満足のため,折紙工学を推進する折紙の展開収縮機能の利用と衝突研究が検討される。
- Origami-performing robot: The optimization of geometrical design of a robot gripper / ○THAI PHUONG THAO (Meiji University), SAVCHENKO MARIA (Meiji University), HAGIWARA ICHIRO (Meiji University) [概要]
Forming the sharp creases, which are represented on the origami crease pattern, by the robotic arms with the end-effectors (grippers), is a challenge. The accuracy of the formed crease lines depends on some design criteria of a robot, such as: a gripper position on the origami paper pattern, geometric sizes of the robot parts, force distributions and so on. In this paper, we consider the buckling of the A4 paper sheets during the forming process of the origami crease lines by the grippers with the limited geometrical sizes. The geometrical approach for the design of the plane contact portion of a robot gripper with a goal to guarantee the flatness of a sheet of paper in the folding area is presented and applied for three A4 paper format orientations on the robot working table: portrait, landscape, and diagonal. The calculated optimal geometric parameters of the contact area of the gripper are unified and can be used for three orientations of the sheet of paper. Practical implementation of the proposed approach is demonstrated by using the simulation software LS-DYNA.
▷ [研究部会OS] 科学技術計算と数値解析 (1) [9月12日:09:30-10:50:2C](座長:山本 野人(電気通信大学))
- Hadamard有限部分積分に対する超函数法 / ○緒方 秀教 (電気通信大学大学院情報理工学研究科 情報・ネットワーク工学専攻) [概要]
特異点を持ち通常の積分が発散するような関数に対しても、発散項を除いた有限値の部分をもって積分値を定義することができ、これをHadamardの有限部分積分と呼ぶ。この有限部分積分は、佐藤超函数の枠組みで考えれば通常の積分と同等の扱いができる。本研究では、この事実に基づいて、通常の積分に対して提案された「超函数法」~佐藤超函数論に基づく数値積分法~の有限部分積分への拡張を提案し、その性能を理論・実験両面から検証する。
- ◎eye-shaped領域上の重み付きハーディ空間における2つの最適な関数近似公式の比較 / ○杉田 幸亮 (青山学院大学大学院理工学研究科 M2), 杉原 正顯 (青山学院大学 理工学部 物理・数理学科), 田中 健一郎 (武蔵野大学 工学部 数理工学科), 岡山 友昭 (広島市立大学 大学院情報科学研究科) [概要]
一重指数関数的重みを持つ重み付きハーディ空間において,「最適な」近似公式として,一般論から導かれた公式 (杉原(2003)) と,Jang- Haberの不定積分公式からヒントを得て構築された公式 (鵜島(2011)) がある.一方,重み付きハー ディ空間上の関数近似に関してポテンシャル論を用いた研究が,田中,岡山,杉原によって進められている.本講演では,関連する最近の研究成果を必要に応じて参照しつつ,近似対象の関数や標本点の取り方等を変えることによって様々な条件下で数値計算を行い,2つの関数近似公式から生じる誤差を比較することによって得られた知見を紹介する.
- 重み付きハーディ空間における高精度数値積分公式の設計 / ○田中 健一郎 (武蔵野大学 工学部 数理工学科), 岡山 友昭 (広島市立大学 大学院情報科学研究科), 杉原 正顯 (青山学院大学 理工学部 物理・数理学科) [概要]
数値積分公式として著名な二重指数関数型(DE)公式は,一定の条件を満たす解析関数に対して極めて有効であり,特に端点特異性に強いことが知られている.このことを理論的に示す際には,DE変換を施した後の被積分関数が,二重指数関数的な重みを持つ重み付きハーディ空間に属すことを仮定するのが一般的である.一方,重み付きハーディ空間では,標本点数を固定した時の数値積分公式の最適性を定義することができる.この定義に基づくと,DE公式が準最適となることが杉原によって示されている.しかし,最適公式やその精度はまだ分かっていない.本研究では,一般的な重みに対する重み付きハーディ空間に対して,まず最適精度の表示式を導出した.そしてその表示式に基づいて,最適に十分近いと考えられる数値積分公式を設計した.なお,この公式では標本点を実軸上にとるものとしている.数値実験では,重みが二重指数関数的な場合について,この公式がDE公式を超える精度を達成することが観察された.
- ◎積分の刻み幅制御を用いたHamiltonian Monte Carlo / ○奥戸 道子 (東京大学), 鈴木 秀幸 (大阪大学) [概要]
Hamiltonian Monte Carlo (HMC)はHamilton系の時間発展の微分方程式の計算をサンプル生成に利用したMCMCであり,数値積分を構造保存的に行うことで高い効率を実現している.本研究では数値積分の刻み幅制御をHMCに適用して,多峰の分布などの難しい分布での収束速度を改善する.HMC計算が必要とする数値積分法の条件や計算時間の要請に合う刻み幅制御のスキームを適用する.
▷ [研究部会OS] 科学技術計算と数値解析 (2) [9月12日:11:00-12:20:2C](座長:今井 仁司(同志社大学))
- ◎変分原理に基づくエネルギー保存数値解法の一般のHamilton系への拡張 / ○石川 歩惟 (神戸大学), 谷口 隆晴 (神戸大学) [概要]
我々はこれまでに変分原理に基づく新しいエネルギー保存数値解法設計法を提案してきた.この方法は,標準的なHamilton方程式のみにしか適用することができなかったが,本発表では,提案手法を一般のHamilton方程式に対して拡張する.
- KdV方程式に対する複数の保存量を再現する差分スキーム / McLaren David (La Trobe University), ○宮武 勇登 (名古屋大学), Quispel G. Reinout W. (La Trobe University) [概要]
偏微分方程式に対して保存量を再現する保存差分スキームの研究では,多くの場合一つの保存量のみを対象とする事が多い.本講演では,無限個の保存量を持つKdV方程式を対象に,複数の保存量を再現するスキームの導出法およびスキームの安定性を示す.
- ◎平面曲線の勾配流に対するB-splineによる構造保存数値解法 / ○剱持 智哉 (東京大学大学院数理科学研究科) [概要]
本講演では, 平面曲線の勾配流, 特に, Willmore流などの高階の方程式に対する構造保存的な数値計算法について述べる. すなわち, エネルギーが減衰する数値解法を構成する. 時間の離散化に関しては離散勾配法をアレンジしたものを用い, 空間の離散化に関してはB-splineを用いる. これにより, 自己交差のあるような初期値に対する方程式であっても, 4階やそれ以上の階数の方程式であっても, 安定した計算をすることができる. 数値例もいくつか紹介する.
- エネルギー保存スキームにおける運動量保存則 / ○佐々 成正 (日本原子力研究開発機構システム計算科学センター) [概要]
QuispelやHairerらによって提唱されている、エネルギー保存
数値計算スキームを用いてHamilton系PDEの時間発展問題を
考える。この時、近似的に成り立つ運動量保存則について考
察をおこなう。
▷ [研究部会OS] 科学技術計算と数値解析 (3) [9月12日:13:30-14:50:2C](座長:土屋 卓也(愛媛大学))
- ◎オーバーラッピング型領域分割に基づくSPIKE前処理 / ○森田 直樹 (東京大学大学院), 橋本 学 (東京大学大学院), 奥田 洋司 (東京大学大学院) [概要]
大規模な連立一次方程式を解くための計算手法として,メニーコア環境に適し,高い並列計算効率を有する点から,SPIKE直接法が注目されている.本研究では,オーバーラッピング型領域分割の情報に基づいて,従来,帯行列にのみ適用可能であったSPIKE直接法の制約を解消する.提案手法は共役勾配法前処理として実装し,並列有限要素法から得られる係数行列を用いた数値例により,計算時間と並列計算効率を検証する.
- メルセンヌツイスタ擬似乱数発生法の連結について / ○原瀬 晋 (立命館大学理工学部) [概要]
32ビット出力のメルセンヌツイスタ法MT19937は最も広く使われている擬似乱数発生法の一つである。特に、C++11以降では、ヘッダで採用され、MT19937を呼び出すことが出来る。そこで、[0,1)上の一様乱数を得る際に、2つの32ビット整数出力を連結して64ビット化し、それを2の64乗で割って倍精度浮動小数点数を得る実装が行われている。本講演では、MT19937の出力を連結した場合の上位ビットの高次元均等分布性について調べる。
- ◎Hybrid力学系の不動点およびLyapunov関数についての精度保証 / ○新田 光輝 (電気通信大学), 中山 大輔 (電気通信大学), 三宅 智大 (電気通信大学), 山本 野人 (電気通信大学) [概要]
連続力学系と離散力学系の組み合わせからなるHybrid力学系と呼ばれる力学系がある。このHybrid力学系に対して、精度保証付き数値計算を用いた二つの解析手法を提案し、数値例を通してその有用性を確認する。一つは、Krawczyk法を基にした不動点の存在検証を行う精度保証法であり、もう一つは不動点周辺でのLyapunov関数の精度保証を用いた構成法である。数値例としては、受動歩行と呼ばれる歩行モデルをHybrid力学系として捉えて、その不動点の検証とLyapunov関数の構成を行う。
- 連続力学系における漸近安定な閉軌道の吸引域に関する精度保証 / 山本 野人 (電気通信大学), ○樋脇 知広 (株式会社AT情報研) [概要]
連続力学系における閉軌道が漸近安定である場合に、その吸引域に含まれる領域を精度保証法によって確定する方法を提案する。既存の方法としては、ポアンカレ写像の不動点の存在検証とそのLyapunov関数の構成をおこなうものがある。これに対し、本手法では不動点の存在と吸引領域とを同時に検証する。講演で数値例を示す。
▷ [研究部会OS] 科学技術計算と数値解析 (4) [9月12日:15:00-16:20:2C](座長:降旗 大介(大阪大学))
- 重調和方程式に対するある混合型有限要素スキームに基づくHDG法 / ○小山 大介 (電気通信大学) [概要]
重調和方程式に対するHermann-Miyoshi法(HM法),Hermann-Johnson法(HJ法)と呼ばれる混合法がある.HM法,HJ法それぞれに基づくHDG法を紹介する.HJ法に基づくHDG法は,HJ法より解の収束率が落ちるが,HJ法の係数行列作成時における連立一次方程式を解く手間を解消できる方法となる.
- 局所線形流速を用いたP1/P1安定化Lagrange-Galerkinスキーム / ○内海 晋弥 (早稲田大学大学院基幹理工学研究科), 野津 裕史 (金沢大学理工研究域数物科学系), 田端 正久 (早稲田大学理工学術院) [概要]
流れ問題に対して有効な計算手法であるLagrange-Galerkinスキームを考える.Lagrange-Galerkinスキームはその定式化と実装との間に乖離があることが問題であったが,最近P2/P1要素に対して,局所線形流速を導入し,数値積分を使うことなく厳密に計算できるスキームが作成された.一方で,P1/P1要素を用い安定化項を加え,少ない自由度で計算できるスキームも作成された.本報告では,これら2つの手法を結合したスキームを述べる.
- Finite element approximation of minimal surfaces / ○Grodet Aymeric (愛媛大学理工学研究科), 土屋 卓也 (愛媛大学理工学研究科) [概要]
3次元ユークリッド空間内に閉Jordan曲線が与えられているとき、それを境界とする単位円板から3次元ユークリッド空間内への極小曲面を求めよという古典的Plateau問題、およびその拡張について考察する。特に、古典的Plateau問題を「極小曲面の境界の一部がある曲面上にある」という形に拡張した自由境界をもつ極小曲面の場合で、区分的1次有限要素近似を考える。この場合に、有限要素解の収束について得られた結果を報告する。数値例も与える予定である。
- 創成解による大変形問題に対する有限要素近似の検証 / ○山田 貴博 (横浜国立大学) [概要]
筆者等は,創成解の方法において創成解から得られるソース項(体積力)を,弱定式化に基づき有限要素法における等価節点力として直接算出する手法を開発し,従来困難だった固体の非線形問題における誤差評価を可能とする手法を提案してきた.本研究は,この手法を用いて,ゴム材料のモデルである超弾性体の大変形問題における有限要素近似の数値特性の評価と計算手法の検証を行う.
▷ [研究部会OS] 機械学習 [9月12日:09:30-10:50:3F](座長:烏山 昌幸(名古屋工業大学))
- 多様体学習に基づく特徴クラスタリング / ○烏山 昌幸 (名古屋工業大学), 馬見塚 拓 (京都大学) [概要]
遺伝子データなど高次元の特徴量を扱う場合には,互いに依存関係のある特徴グループを抽出することで特徴間の相互作用の発見やその後の解析に役立てることができる.本発表では,多様体学習を用いて多次元の特徴空間を共通の多様体を共有するグループに分割する方法を紹介する.
- 非線形動的システムのスペクトル学習 / ○河原 吉伸 (大阪大学) [概要]
時系列データを用いた動的システム(状態空間モデル)の推定・分析は,様々な工学的・科学的領域において基礎となる重要な問題である.本講演では,非線形動的システムにおけるこの問題へのカーネルを用いたスペクトル学習に基づくアプローチについて述べるとともに,関連する最近の話題についてもふれる.
- オンライン転移学習と医用画像読影支援への応用 / ○佐藤 一誠 (東京大学), 野村 行弘 (東京大学), 林 直人 (東京大学) [概要]
学習データの少ない領域で学習する際に,他の利用可能な領域における学習データを用いることで学習効率を上げる手法は転移学習と呼ばれている.本研究では,ドメイン間でデータの共有ができない場合における転移学習を対象とし,負の転移に関する理論的な保証を与える学習手法を提案する.また具体的な応用として,異なる病院間での脳動脈瘤検知問題に対して,提案手法の有用性を説明する.
- 走査型電子顕微鏡データ解析のための非負値行列分解 / ○志賀 元紀 (岐阜大学), 武藤 俊介 (名古屋大学), 巽 一厳 (名古屋大学), 津田 宏治 (東京大学) [概要]
物質・材料の計測機器の目覚ましい発達しており、特に、走査型電子顕微鏡の発達は目覚ましく、評価試料面の各点において化学状態や元素成分を反映するスペクトルを原子スケールで自動的に取得できるようになってきた。発表者らは、自動計測された膨大なデータの解析を自動化する試みており、本発表では、計測データから試料平面上に元素成分を自動的にマッピングするための非負値行列分解法を紹介する。
▷ [研究部会OS] 行列・固有値問題の解法とその応用(1) [9月13日:09:30-10:50:2C](座長:保國 惠一(筑波大学))
- ◎SVRG 法のグラスマン多様体上への拡張とその行列補完問題への応用 / ○佐藤 寛之 (東京理科大学), 笠井 裕之 (電気通信大学), MISHRA Bamdev (Amazon Development Centre India) [概要]
目的関数がサンプル毎に分割可能で,そのサンプル数が非常に大きい場合の最小化問題の解法として,サンプルを確率的に選択して対応する勾配を用いる確率的勾配降下法(SGD)がある.本講演では,確率的勾配を用いて計算される探索方向の分散が小さくなるよう SGD を改良した解法である SVRG をリーマン多様体上に拡張する.また,提案アルゴリズムの収束性を議論し,グラスマン多様体上の低ランク行列補完問題への応用を数値実験結果とともに紹介する.
- An Alternating Modulus Nonnegative Least Squares Method for Nonnegative Matrix Factorization / ○Zheng Ning (SOKENDAI (The Graduate University for Advanced Studies)), Hayami Ken (National Institute of Informatics, SOKENDAI (The Graduate University for Advanced Studies)) [概要]
For the solution of nonnegative matrix factorization, we propose a new alternating nonnegative least squares method
by utilizing modulus method to solve the nonnegative constrained least squares problem in each iteration. Numerical results show that the proposed method converges faster than the popular multiplicative update method.
- 射影手法を導入した正定行列束判定の高速化 / ○足立 智 (東京大学), 中務 佑治 (University of Oxford) [概要]
2つの対称行列が線形和により正定値行列にできるとき,それらは正定行列束であるという.本発表では正定行列束判定の既存手法に対し反復回数を削減する初期値を与えるため,射影操作を導入する手法を提案する.この操作により反復回数を半分程度に減らせることを数値実験で示す.
- ◎行列指数関数のためのShift-invert Rational Krylov法 / ○橋本 悠香 (慶応義塾大学大学院理工学研究科), 野寺 隆 (慶応義塾大学理工学部) [概要]
大規模行列指数関数に対して,Shift-invert Arnoldi法やRational Krylov法による近似が行われてきた.本講演では,Rational Krylov法に対する新しい考察を与え,それを基に適切なシフトのとり方と近似の仕方を提案する.そして,得られる誤差の上界が1次以上の速さで減少していくことを示す.
▷ [研究部会OS] 行列・固有値問題の解法とその応用(2) [9月13日:11:00-12:20:2C](座長:佐藤 寛之(東京理科大学))
- GKB-GCV法を用いた多変量画像のぼやけ除去 / ○富樫 大 (慶應義塾大学大学院), 野寺 隆 (慶應義塾大学) [概要]
近年、白黒画像のぼやけ除去問題を高速に解くGKB-GCV法を提案した。今回、多変量画像のぼやけ除去問題に対しGKB-GCV法の拡張を提案し、数値実験の結果と今後の課題について述べる。
- クラスタ行列に対する高精度特異値分解を実現するシフト戦略について / ○荒木 翔 (京都大学), 木村 欣司 (京都大学), 中村 佳正 (京都大学) [概要]
Wilkinson行列に似た複数のクラスタを持つ上2重対角行列は, 数値計算ライブラリLAPACKの分割統治法によってその特異値分解を得られないことが知られている.
本発表では, 上記の行列を含む種々の行列に対する一般化Rutishauserシフト戦略およびコラッツの定理に基づくシフト戦略を採用した直交QD法の数値実験の結果を示し,これらのシフト戦略と計算速度や分解精度といったアルゴリズム特性との関係について考察する.
- 新しいシフト戦略に基づく直交QD法の簡約操作から定式化されるdqds法について / ○木村 欣司 (京大情報), 中村 佳正 (京大情報) [概要]
新しいシフト戦略に基づく直交QD法の実装から特異ベクトルの計算機能を取り去ったことによって生成されるdqds法の実装が, クラスタ行列を含めたさまざまなテスト行列に対して, 高い性能を発揮できることを確認する.
- 直交QD法を下位ルーチンとして用いるthick-restart Golub-Kahan-Lanczos法の実装と性能評価 / ○石田 遊也 (京都大学大学院情報学研究科), 木村 欣司 (京都大学大学院情報学研究科), 中村 佳正 (京都大学大学院情報学研究科) [概要]
著者らによる直交QD法を、部分特異対分解アルゴリズムであるthick-restart Golub-Kahan-Lanczos法の下位ルーチンとして用いた場合の実装と性能評価を報告する。
▷ [研究部会OS] 行列・固有値問題の解法とその応用(3) [9月13日:13:30-14:50:2C](座長:多田野 寛人(筑波大学))
- クリロフ部分空間法による物質科学のためのオープンソース・アプリケーション / ○山地 洋平 (東京大学), 三澤 貴宏 (東京大学), 吉見 一慶 (東京大学), 河村 光晶 (東京大学), 藤堂 眞治 (東京大学), 星 健夫 (鳥取大学), 曽我部 知広 (名古屋大学), 川島 直輝 (東京大学) [概要]
クリロフ部分空間法の数理と物質科学を繋ぐことを目指して開発を進めている量子多体問題アプリケーションHΦについて紹介し、量子多体問題の中間固有状態をターゲットとした疎行列固有値問題とその応用を示す。
- 逆一般化固有値問題に対する擬似ニュートン法 / ○相島 健助 (東京大学) [概要]
逆固有値問題とは,指定した固有値とある種の構造をもつ行列を求める問題であり,ニュートン法が代表的な数値解法になる.本発表では,一定の条件下で一般化固有値問題に対する逆問題にも適用可能な擬似ニュートン法を提案する.
- ◎長方行列束の固有値問題に対する周回積分型解法 / ○保國 惠一 (筑波大学) [概要]
複素平面上の指定された領域内部における, 長方行列束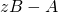 ,
, 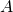 ,
, 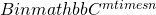 のすべての固有値
のすべての固有値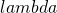 および対応する固有ベクトル
および対応する固有ベクトル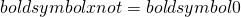 を求める固有値問題
を求める固有値問題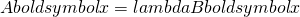 に対する周回積分型解法を提案する. 提案法の定式化を示し, 数値実験で有効性を示す.
に対する周回積分型解法を提案する. 提案法の定式化を示し, 数値実験で有効性を示す.
- レゾルベントの多項式をフィルタに用いた対称定値一般固有値問題のフィルタ対角化法 / ○村上 弘 (首都大学東京) [概要]
フィルタ対角化法で対称定値一般固有値問題を解くために使用するフィルタとして、レゾルベントの多項式を用いる場合につい考察を行なう。
▷ [研究部会OS] 計算の品質(1) [9月14日:09:30-10:50:2B](座長:高安 亮紀(筑波大学))
- Legendre多項式による重調和方程式の精度保証付き誤差評価 / ○渡部 善隆 (九州大学), 木下 武彦 (京都大学), 中尾 充宏 (九州大学) [概要]
重調和方程式の境界値問題に対し有限次元近似解の数学的に厳密な誤差上界を構成的に評価する精度保証付き数値計算手法を提案します。従来の手法と現状における問題点を延べ、Legendre多項式を用いた基底による構成的誤差評価方法を具体的な数値例とともに紹介します。
- Stokes微分作用素の厳密な固有値評価について / ○劉 雪峰 (新潟大学) [概要]
以下のStokes微分作用素の固有値問題はNavier-Stokes微分方程式の線形化問題に密接している。本研究では適合有限要素法と非適合有限要素法(Crouzeix-Raviart要素)を巧妙に利用することで、一般的な多角形領域 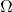 におけるStokes微分作用素の固有値に対して、厳密な上下界の評価を得た。
におけるStokes微分作用素の固有値に対して、厳密な上下界の評価を得た。
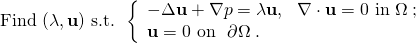
- ◎Slow manifoldの「滑らかな近傍」の精度保証付き数値計算 / ○松江 要 (統計数理研究所) [概要]
マルチスケールダイナミクスの一種であるfast-slow systemにおいて中心となる幾何学的対象:slow manifoldの近傍の精度保証付き数値計算について考察します。Slow manifoldの同定に加えて、多様体の各点に連続依存する線型化行列の固有対の精度保証付き数値計算も組み合わせる事で、slow manifoldの各点を中心とし、与えられた半径を持つ管状近傍、錐型近傍、星型近傍を構成する事ができます。これにより、fast-slow systemの計算機援用解析が劇的に簡単になります。
- ◎Lotka-Volterra型偏微分方程式の初期値境界値問題の解に対する精度保証付き数値計算法について / ○水口 信 (早稲田大学 基幹理工学研究科), 関根 晃太 (早稲田大学 理工学術院), 大石 進一 (早稲田大学 理工学術院) [概要]
本講演ではLotka-Volterra型偏微分方程式の初期値境界値問題の解に対する精度保証付き数値計算法について論じる. ラプラス作用素に非線形項のフレッシェ微分の摂動を加えた微分作用素から生成される半群を使い, ある不動点形式を導入する. Banachの不動点定理から解の存在に関する十分条件を導き, その条件が成立しているかチェックすることで解の存在を検証する.
▷ [研究部会OS] 計算の品質(2) [9月14日:11:00-12:20:2B](座長:渡部 善隆(九州大学))
- CUDAの丸めモード指定演算を用いた行列積の高速な包含方法 / ○森倉 悠介 (早稲田大学), 野澤 優介 (早稲田大学), 関根 晃大 (早稲田大学), 柏木 雅英 (早稲田大学), 大石 進一 (早稲田大学) [概要]
CPUでは丸めの向きをグローバルに変更することができるが,GPUでは1回の演算に対しての丸め方向を変更する命令しかない.本講演では,CUDAの丸めモード指定演算を用いた行列積の高速な包含方法について述べる.
- ◎ハウスホルダーQR分解を用いた連立一次方程式の数値解に対する精度保証 / ○柳澤 優香 (早稲田大学 理工学研究所), 大石 進一 (早稲田大学), 野田 ふみ (早稲田大学) [概要]
連立一次方程式の近似解を計算する手法は多数存在するが,部分ピボット選択付きLU分解を用いた方法が一般的である.一方,ハウスホルダーQR分解は数値安定性に優れた方法であるが,近似解を計算するにはLU分解の2倍の計算量が必要なため,計算量の観点においてはLU分解の方がメリットがある.しかしながら, 精度保証の手間を合わせると, QR分解を用いた精度保証法は,LU分解を用いた方法と同程度の計算量で,かつ,精度が良いことがわかった.本発表では, QR分解に基づく連立一次方程式の精度保証付き数値計算法を説明し,アルゴリズムの解析,及び,難しい問題(悪条件性問題)の取り扱いも含めて数値実験を行った結果を示しその考察を行う.
- ◎On verified bounds of ill-posed linear programming problems / ○Lange Marko (Waseda University) [概要]
In an earlier work, Ordóñez and Freund have shown that 71% of the instances from the Netlib test suite – a benchmark suite consisting of difficult but practically relevant linear programming problems – have infinite condition measure. Due to their practical background and possible inaccuracies in the input data, these problem instances are very interesting for the application of verification methods.
However, the computation of verified bounds for these ill-posed programming problems is typically considered as an extremely difficult task. In this work, we are proposing an error free preprocessing procedure for the generation of equivalent problem instances which are well-posed.
We demonstrate the applicability of our procedure by computing new verified bounds for a large number of ill-posed problem instances from the Netlib test suite, comparing our results with the bounds by Keil and Jansson.
- 3つの行列の積に対する区間包囲法 / ○中村 吉宏 (芝浦工業大学), 太田 悠暉 (芝浦工業大学), 尾崎 克久 (芝浦工業大学) [概要]
本発表では,3つの点行列の積に関する区間包囲法について述べる.2つの点行列の積については,近年効率的な区間包囲法が多く開発された.3つの点行列の積について,2つの積に関する方法を組み合わせて区間包囲法を開発すると,32通りの手法が存在する.その中で効率的な方法について調べた結果を発表する.特に計算量が多くてもタイトな区間を得られない手法についての注意も述べる.
▷ [研究部会OS] 計算の品質(3) [9月14日:13:30-14:50:2B](座長:劉 雪峰(新潟大学))
- 高精度な総和計算アルゴリズムにおける無誤差変換の改良 / ○南畑 淳史 (早稲田大学), 尾崎 克久 (芝浦工業大学 and JST, CREST), 荻田 武史 (東京女子大学 and JST, CREST), 大石 進一 (早稲田大学 and JST, CREST) [概要]
浮動小数点数の和を考えることは、最も根本的な問題である。浮動小数点数の和は丸め誤差により、必ずしも正確な答えを得られるわけではない。丸め誤差を避けるために、浮動小数点フォーマット以外を使う場合は高速性が失われる。そこで、浮動小数点の計算を使いつつ、高精度な浮動小数点数の和を求める方法が提案されている。本発表ではOgita-Rump-Oishiが提案したアルゴリズムの性能を向上させる方法を提案する。
- 無誤差演算のための最小演算精度による高精度演算の高速化とその評価 / ○井川 尚幸 (九州工業大学), 古賀 雅伸 (九州工業大学) [概要]
本研究では、多倍長演算において四則演算結果を無誤差で得るために必要な最小演算精度を導出する手法を提案し、例題を用いて評価する。通常、無誤差変換を繰り返し用いると必要とする演算精度が増えてしまうが、我々が提案する手法を用いることにより演算精度の増加が抑制され、減少するケースもあるため演算の高速化や使用メモリの抑制が可能になる。
- 部分積分とEuler-Maclaurinの公式を用いたベキ型特異点を持つ関数の精度保証付き数値積分 / ○小林 領 (早稲田大学 基幹理工学研究科), 関根 晃太 (早稲田大学 理工学術院), 柏木 雅英 (早稲田大学 理工学術院), 大石 進一 (早稲田大学 理工学術院、CREST/JST) [概要]
ベキ型特異点を持つ関数に対する精度保証付き数値積分を考える。まず、台形公式に基づくオイラーマクローリンの公式を用いた精度保証付き数値積分法を提案する。さらに、この方法は積分区間でベキ型特異点を持つ場合には直接用いることができないため、部分積分を用いて特異点を持たない関数の積分を導いてから、前述の精度保証付き数値積分法を用いる方法を提案する。
- 精度保証付き二重積分について / ○高橋 侑希 (早稲田大学), 柏木 雅英 (早稲田大学) [概要]
精度保証付き二重積分の計算方法を二種類提案する。一つ目は二重べき級数展開による方法で、変数を二重べき級数展開の形で持たせ演算し積分する。二つ目は、ニュートン・コーツの積分公式の誤差評価式を用いて二次元に拡張させたものである。
▷ [研究部会OS] 計算の品質(4) [9月14日:15:00-16:20:2B](座長:柳澤 優香(早稲田大学))
- 連立一次方程式の数値解のためのテスト問題の生成法 / ○尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
本研究発表では,連立一次方程式の数値解の精度を検証するためのテスト問題の生成法について提案する.成分がすべて浮動小数点数である係数行列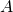 と解ベクトル
と解ベクトル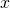 が与えられ,
が与えられ,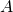 に近い行列
に近い行列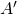 を生成し,
を生成し,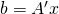 の計算に誤差がないようにすることにより,厳密に
の計算に誤差がないようにすることにより,厳密に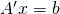 を満たす.厳密解がわかる連立一次方程式は,精度保証が与える誤差限界の妥当性の検証や,反復解法の挙動解析などに役立つと考えられる.
を満たす.厳密解がわかる連立一次方程式は,精度保証が与える誤差限界の妥当性の検証や,反復解法の挙動解析などに役立つと考えられる.
- ◎2次元平面における2点間の距離の大小判定問題に関する精度保証法 / ○太田 悠暉 (芝浦工業大学), 尾崎 克久 (芝浦工業大学) [概要]
本発表では,2次元平面にある3点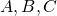 に対して,点
に対して,点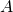 からの距離が近いのが
からの距離が近いのが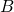 か
か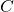 かを判断する問題を考える.
これは,計算幾何学の分野において応用が多い問題の1つである.
しかし,数値計算によって判定を行うと丸め誤差の影響で,誤判定をする可能性がある.
そこで,誤判定になりそうな入力とそれ以外に分ける、浮動小数点フィルタを開発した.
また,浮動小数点フィルタをベースにした最近傍探索のアルゴリズムを開発した.その実験結果等について発表で述べる.
かを判断する問題を考える.
これは,計算幾何学の分野において応用が多い問題の1つである.
しかし,数値計算によって判定を行うと丸め誤差の影響で,誤判定をする可能性がある.
そこで,誤判定になりそうな入力とそれ以外に分ける、浮動小数点フィルタを開発した.
また,浮動小数点フィルタをベースにした最近傍探索のアルゴリズムを開発した.その実験結果等について発表で述べる.
- ◎前処理を用いた悪条件連立一次方程式の高精度な数値計算法 / ○小林 由佳 (東京女子大学大学院), 荻田 武史 (東京女子大学) [概要]
倍精度演算を用いたLU分解と前進後退代入によって高精度な数値解が得られないような悪条件連立一次方程式を考える。LU分解の結果を用いた前処理法に基づき、係数行列の特異値の分布に応じて従来よりも高速に高精度な数値解を得ることができるアルゴリズムを提案する。
▷ [研究部会OS] 産業における応用数理 [9月12日:16:30-17:50:1A](座長:櫻井 鉄也(筑波大学))
- 大規模グラフ解析と都市 OS の開発 —ヒト・モノのモビリティに関する新しい数理モデルとその応用— / ○藤澤 克樹 (九州大学) [概要]
新しいスーパーコンピュータの応用として大規模なグラフ解析が注目を集めている. 現在、都市 OS 開発などのサイバーフィジカルシステムにおいて、ヒト・モノのモビリティに関する数理モデル及び最適化手法としてのグラフ解析の利用が開始されている。このような最先端理論(Algorithm Theory)+ 大規模実データ(Big Data)+ 最新計算技術(Computation)の有機的な組合せによる最新のグラフ解析の応用について紹介を行う.
- ◎劣加法性に基づく提携構造形成問題とその応用 / 神山 直之 (九州大学, JSTさきがけ), ○吉良 知文 (九州大学), 穴井 宏和 ((株)富士通研究所), 岩根 秀直 ((株)富士通研究所), 大堀 耕太郎 ((株)富士通研究所) [概要]
協力ゲームでは,通常,プレーヤー全員が協力する前提(特性関数の劣加法性)で公平な費用負担が議論される.一方,現実には個人的に損をする者が存在し,全体最適であっても協力が実現しない.全員を協力が成立する部分集合に上手く分割できれば,既存理論を適用し協力を促すことができる.本研究では,協力が成立する分割数最小の分割を求める最適化問題を定式化し,近似解法と相乗り運行計画立案への応用を述べる.
- 剛体・油圧連成解析を用いた電動機HILSシステムの開発 / ○今西 悦二郎 (神戸製鋼) [概要]
直動要素で駆動される剛体システムを用いた電動機のHILS評価手法を提案する.電動機にリアルタイムな負荷を作用させることによって,電動機の特性を評価する手法を示した.
- 複素モーメント型並列固有値解法の耐障害性とその性能評価 / ○今倉 暁 (筑波大学), 二村 保徳 (筑波大学), 櫻井 鉄也 (筑波大学) [概要]
近年のスーパーコンピュータの大規模・高性能化に伴いシステムの故障率が向上しており,長時間シミュレーションの困難さが懸念されている.このため,システムレベルでの対策とともに,アルゴリズムレベルでの耐障害性の実現が必要不可欠である.本講演では,近年注目を集める複素モーメント型超並列固有値解法に焦点を当て,アルゴリズムレベルでの耐障害性を実現し,その性能評価を行う.
▷ [研究部会OS] 数理医学 [9月14日:13:30-14:50:2D](座長:鈴木 貴(大阪大学))
- ◎数理モデルによる心筋細胞の集団効果の解析について / ○林 達也 (東京大学大学院数理科学研究科), 時弘 哲治 (東京大学大学院数理科学研究科), 栗原 裕基 (東京大学大学院医学系研究科), 野村 典正 (東京医科歯科大学生体材料工学研究所), 安田 賢二 (早稲田大学理工学術院先進理工学部) [概要]
最近の実験技術の進歩により,心筋細胞をチップ上に1細胞単位で配置し,細胞集団のネットワークを構築することで,心筋細胞の拍動同期や細胞集団のサイズの効果について詳しく調べることが可能になった.今回は,安田研究室で行われた心筋2細胞の拍動同期実験の観測結果から構築した数理モデルを用いて,心筋細胞の集団効果を調べるin silicoの実験を行ったので,その結果について報告する.
- 核内パターン形成における動的変形空間の役割 / ○李 聖林 (広島大学), 落合 博 (JST) [概要]
細胞は、自己組織化を通じて自らの機能を制御する。無論、その機能制御には、遺伝子と言う設計図が基になっている。そこで、細胞の機能制御の仕組みというのは、設計図となる遺伝子を解析すれば、全て分かるものだろうか。しかし、そうではない。細胞は下層の設計図を基にした上層の様々な仕組みを自らの機能を的確に制御するために、巧みに利用している。その一つが遺伝子が作りだす空間的パターンである。例えば、昼行性哺乳類と夜行性哺乳類のそれぞれの網膜にある桿体細胞の核では、全く異なる遺伝子発現の分布が見られる。それらの空間的パターンは、桿体細胞が光を集める機能を果たすことに重要に関わっている。また、夜行性動物の核のパターンは昼行性動物の核のパターンからの連続的変化により獲得される事が明らかになったが、その仕組みについては全く謎のままである。本講演では、その謎を遺伝子が置かれている空間(核)の動的変形から紐解いていく。本研究は数理モデルでの理論的考察に留まらず、In vitro 実験の検証に成功し、生物学的に新しい発見を見出しており、生命科学における数理の新しい役割を提案していく。
- EGFR,ERBB の重合に関する数理モデルと解析 / ○板野 景子 (大阪大学) [概要]
膜分子EGFR,ERBB Familyの重合体は、乳がん、脳腫瘍、心臓の肥大等重篤な病気を引き起こす、もしくは抑制する等、重要な役割を果たす。
しかし、そのメカニズムについては解明されていないことも多い。
がんを誘発するERBBの重合体形成を例に、このパスウェイネットワークに阻害剤を投入した場合の結合解離の反応を数理モデルで表現し、ネットワークの挙動やターゲットとなるERBB重合体を抑制に重要なパラメーターの特定を行う。
- 離散と連続の入り混じった相互情報量を推定して、 SNPと遺伝子発現量の因果関係をさぐる / ○鈴木 譲 (大阪大学) [概要]
遺伝子の発現量とSNPのデータから、相互情報量の推定量を用いて、 それらの因果関係をさぐる。離散と連続の変数が混在しているため相互情報量が推定は容易ではなく、既存研究でもグラフィカルモデルのクラスを制限している。本研究では、新しい推定量を提案し、精度と計算量を数学的に保証している。、
▷ [研究部会OS] 数理政治学 [9月12日:09:30-10:50:2D](座長:大山 達雄(政策研究大学院大学))
- 原理党を含む展開系ゲームの部分ゲーム完全均衡解の解析的記述 / ○岸本 一男 (筑波大学システム情報系) [概要]
空間的投票理論でのダウンズ・モデルで原理党を含む場合を展開系ゲームとして扱い,政党の政策位置を部分ゲーム完全均衡によって記述されるとした場合に,解析的に均衡解を表現できる場合について,その解を具体的に記述する.
- アダムズ方式は人口比例配分を実現するのか / ○一森 哲男 (大阪工業大学) [概要]
最近の選挙制度改革のキーワードはアダムズ方式である.マスコミはこれを人口比例する議席配分方式,あるいは,格差を小さくする配分方式ともてはやしているが,はたして,実態はどうであるのか.我が国の現実の人口データを用いて,この点を検討する.
- Investigating the Japanese Election System through Recent National Elections / ○大山 達雄 (政策研究大学院大学) [概要]
First we briefly explain Japanese political and election systems. Then regarding voting ratios by prefectures we show regional characteristics how they are classified with respect to the degree of urbanization. We try to measure the voting efficiency for each political party using pass votes and fail votes data. Regarding the Vote-Share (VS) and Seat-Share (SS) we try to apply the approximation function in order to obtain the relation between VS & SS. Finally, summarizing conclusion is given.
▷ [研究部会OS] 数理設計 [9月14日:15:00-16:20:1A](座長:代田 健二(愛知県立大学))
- ◎拡散方程式を利用した表面積最小化問題の解法 / ○村井 大介 (豊田中央研究所), 近藤 継男 (豊田中央研究所), 川本 敦史 (豊田中央研究所) [概要]
反応拡散方程式を用いて、体積が制約された条件下で物体の表面積を最小化する形状最適化問題の解を求めた。講演では目的関数を表面積とした場合の形状感度の導出、計算結果と実際の最適解の整合性について紹介する予定である。
- Navier-Stokes 流れ場の安定性に関する形状最適化問題 / ○桐山 恭幸 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]
Navier-Stokes流れ場が定常から非定常に遷移するReynolds数(臨界Reynolds数)を最大化することを目指した形状最適化問題を構成して,その数値解法を示す.状態決定問題には定常Navier-Stokes問題とかく乱固有値問題が使われる.評価関数には最大固有値が使われる.また,孤立物体まわりの流れ場に対する形状最適化の数値例を示す.
- 密度型位相最適化問題における評価関数の2階微分と H1 Newton 法 / ○福岡 福治 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]
密度型の位相最適化問題において,評価関数の2階微分の評価方法を示し,それを用いたNewton法を提案する.また,線形弾性体の体積制約つき平均コンプライアンス最小化問題に対する数値例によってその性能を評価する.
- 形状最適化問題における評価関数の2階微分と H1 Newton 法 / ○古木 謙人 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]
領域変動型の形状最適化問題において,評価関数の2階微分の評価方法を示し,それを用いたNewton法を提案する.また,線形弾性体の体積制約つき平均コンプライアンス最小化問題に対する数値例によってその性能を評価する.
▷ [研究部会OS] 数理的技法による情報セキュリティ [9月12日:11:00-12:20:2D](座長:山本 光晴(千葉大学) )
- 複数回の攻撃があるセキュリティゲーム / ○竹内 泉 (産業技術総合研究所) [概要]
従来のセキュリティゲームの研究では、単位期間内に丁度一回の攻撃があるという仮定があった。本研究では、単位期間内に複数回の攻撃があるゲームをモデル化した。そのゲームでは防御側にとって、ナッシュ均衡を構成する戦略と的最大利得最小化戦略が一致することを証明した。
- ◎ProVerifでの形式化における技術的な注意点について / ○荒井 研一 (長崎大学), 岡崎 裕之 (信州大学) [概要]
ProVerifはBlanchetらが開発した形式モデル(Dolev-Yaoモデル)での暗号プロトコルの安全性自動検証ツールであり,暗号プロトコルに要求される秘匿や認証などの安全性要件を検証することができる.SCIS2016において,著者らはProVerifでの形式化に対して暗号プリミティブをプロトコルの一種とみたてることで,暗号プリミティブおよび安全性要件の表現(記述) 能力を向上させ,さらにProVerif自身の検証器を用いて形式化の妥当性を評価・検証する方法を提案した.本発表では,前述の形式化を進める上で発見した,ProVerifでの形式化における技術的な注意点について述べる.
- A Note on Using Sigma Protocols in Cryptographic Protocols / Sakurada Hideki (NTT), Yoneyama Kazuki (Ibaraki University), Hanatani Yoshikazu (Toshiba), ○Yoshida Maki (NICT) [概要]
At Eurocrypt 2011, Lindell proposed efficient universally composable (UC) commitment schemes based on a Sigma protocol. Though it was claimed that one of these schemes is adaptively secure, an attack that violates the blinding property was found via an algebraic property of the Sigma protocol. In this paper, we formalize this property of the Sigma protocol as a general form beyond the algebraic structure, called replicability, and show that representative Sigma protocols are replicable. This means that we need to take into account a similar flaw in the use of Sigma protocols.
▷ [研究部会OS] 数理ファイナンス(1) [9月12日:13:30-14:50:2D](座長:山中 卓(日本銀行))
- 市場で観測できない要因を考慮した信用ポートフォリオのリスク管理について / ○廣中 純 (野村アセットマネジメント株式会社) [概要]
市場で観測可能なファクターおよび直接観測できないファクターとを考慮した信用イベントの強度を表すモデルを提案し、金融機関における信用ポートフォリオの管理を行うために必要と考えられる、日本のクレジット市場全体の信用リスクの変動に対する説明を試みる。また、市場で直接観測できないファクターを駆動する要因がマクロ経済要因の変動等にも起因する点について説明する。
- Optimal portfolio problem in discrete variables with multiple stochastic processes / ○石村 直之 (中央大学商学部), 吉田 直広 (一橋大学大学院経済学研究科) [概要]
最適Portfolio問題を,2つの独立な離散過程のもとで考察する。1つの離散過程はRandom Walkであり,もう片方はPoisson過程である。離散型Ito公式を定式化し,さらに最適性の必要条件である離散型のHamilton-Jacobi-Bellman方程式を導出した。実例によればうまく解ける場合のあることが確認された。離散から連続への収束についても触れたい。
- Local Risk Minimization and Delta Hedging Strategy for Exponential Lévy Models / ○今井 悠人 (早稲田大学) [概要]
We discuss the differences of local risk minimization (LRM) and delta hedging strategies, in exponential Lévy models, where delta hedging strategies in this paper are defined under the minimal martingale measures (MMM). First of all we give inequality estimations for the differences of LRM and delta hedging strategies. Then we show numerical examples for the two typical exponential Lévy models, Merton models and variance Gamma (VG) models.
- 2曲線の間のパス空間に制限されたWiener汎関数積分に対する微分連鎖律とバリア・オプションのGreeksの解析的評価方法 / ○石谷 謙介 (首都大学東京) [概要]
本講演では,2曲線の間のパス空間に制限されたWiener汎関数積分に対する微分連鎖律を用いてバリア・オプションの感応度(Greeks)を解析的に評価する方法を提案する。講演では,Black-Sholesモデルに従う原資産価格過程があらかじめ定められた期間中に上下2つのバリアの何れか一方に達するとオプションの権利が消滅するノックアウト・オプションについて考察する。ペイオフ関数がヨーロッパ型であり,上下のバリアが時間変数に関して定数関数の場合は,ノックアウト・オプションのGreeksの計算公式は既に知られている。一方で,一般のペイオフ関数の場合や上下のバリアが時間曲線の場合にノックアウト・オプションのGreeksを解析的に計算する方法はこれまで知られておらず,またこのGreeksはノックアウト・オプションの理論価格のパラメータ微分であるためモンテカルロ法で高精度に近似することも困難であった。そこで本講演では,バリア・オプションのGreeksを2曲線の間に制限されたWiener汎関数積分に対する微分連鎖律を用いて解析的に計算する手法を提案し,その有効性を示す。更に,この微分連鎖律においてあらわれる境界項の具体形を紹介し,境界項を特徴付ける測度は上下2つのバリア曲線のいずれかにちょうど1回だけ触れるパスの集合上に台(support)を持つことを示す。
▷ [研究部会OS] 数理ファイナンス(2) [9月12日:15:00-16:20:2D](座長:石村 直之(中央大学))
- 受注情報に基づく構造型信用リスク評価モデル / ○山中 卓 (日本銀行) [概要]
企業の受注情報からその企業価値が算出され,企業価値と負債額の比較によって企業のデフォルト発生が決まるという構造をもつ信用リスク評価モデルを提案する.数値例を通して,モデルの有用性を検証する.
- 日経平均先物の注文時間間隔の確率分布の実証分析 / ○橋本 直樹 (筑波大学大学院 システム情報工学研究科 社会工学専攻), 呉 麒 (シンプレクス株式会社), 朱 麗枚 (南京銀行上海分行), 乾 孝治 (明治大学 総合数理学部), 岸本 一男 (筑波大学 システム情報系) [概要]
株式市場の株価変動を忠実に再現することは,自動売買を含めてマーケットの理解に重要である.その基本となるものに,株式の取引発生の確率過程が挙げられる.そこで本研究では,ミリ 秒単位の株式時系列データを用いて,大阪証券取引所の日経平均先物の取引時間間隔の分布を検証した.その結果,取引時間間隔はパレート分布IIIが比較的良い結果を与えることがわかった.
- 企業間のネットワークを考慮した、追加的倒産確率(Additional PD)の提案 / ○金子 拓也 (国際基督教大学), 久門 正人 (金融庁) [概要]
これまで、金融機関の与信の際などに行われる企業の財務審査では、企業単体の決算書などに基づく分析がなされてきた。しかし、当然のことながら企業は単体で存在するわけではなく、さまざまな商取引(ネットワーク)を通じて、複数の他企業と密接な関係が存在しており、今後、それらを考慮した評価が必要になってくるものと我々は考えている。本発表では、企業を取り巻くネットワークを考慮して分析すると、通常の倒産確率に加えて、どの程度追加的に、倒産確率を見積もるべきであるのかを数値化した、追加的倒産確率(Additional Default Probability)について説明し、その計算結果などを紹介する。
▷ [研究部会OS] 数理ファイナンス(3) [9月12日:16:30-17:50:2D](座長:石谷 謙介(首都大学東京))
- ◎Remarks on martingale methodologies for utility maximizations in incomplete markets / ○吉田 直広 (一橋大学大学院経済学研究科) [概要]
本報告は非完備市場における期待効用最大化問題に対するマルチンゲール法に関して,最適戦略の計算方法を中心として,いくつか新しい結果を紹介するものである.まず,連続時間の非完備市場におけるマルチンゲール法を従来よりもいくらか直観的な方法で定式化する.その後,その定式化された問題に対する最適な取引戦略の候補が,適当な仮定のもとで,完備市場における方法を援用することで求められることを説明する.
- Robbins-Monro法を用いたHestonモデルのリスク量計算に関する数値的考察 / ○若林 昌平 (法政大学), 安田 和弘 (法政大学) [概要]
O. Bardou, N. Frikha, G. Pages[2009]では確率的勾配降下法の一つであるRobbins-Monro法を用いることでリスク量(VaRとCVaR)を効率良く求めることができると報告されている.本発表では確率的ボラティリティモデルであるHestonモデルに適用した結果について紹介する.ここでは,モンテカルロ法とRobbins-Monro法,分散減少法を用いた改良Robbins-Monro法の3つの数値実験結果を比較し考察していく.
- ◎フィルタリングを用いたデフォルト強度の推定精度について / ○蛇口 紘史 (法政大学大学院理工学研究科), 安田 和弘 (法政大学) [概要]
Frey, Runggaldier [2010]で, デフォルト強度が観測できないファクター(マルコフ連鎖)に依存する場合に, デフォルトの有無とクレジットデリバティブ価値の情報を用いた, フィルタリングによるデフォルト強度の推定手法が提案された. 本講演ではマルコフ連鎖の状態確率モデルのパラメータに誤差が含まれた場合に, デフォルト強度の推定結果が受ける影響について, 平均二乗誤差と平均絶対誤差の観点から考察する.
▷ [研究部会OS] 数論アルゴリズムとその応用(1) [9月12日:13:30-14:50:3F](座長:内田 幸寛(首都大学東京))
- F4アルゴリズムを用いた2次多変数連立方程式の求解の高速化 / ○伊藤 琢真 (首都大学東京), 内山 成憲 (首都大学東京) [概要]
多変数連立方程式の解を求める手法の1つとしてF4アルゴリズムがある。
ここでは、特に2次多変数連立方程式に対して、このF4アルゴリズムを基に並列化やS多項式の還元方法などの工夫による高速化を提案し、さらにその効果について考察する。
また、量子計算機を用いた攻撃に耐性を持つといわれている暗号系に、多変数公開鍵暗号(MPKC)があり、MPKCの安全性を調べるためにMQChallengeというコンテストが行われているが、その問題への提案手法の適用についても述べる。
- ◎体上の多項式環におけるオイラー素数の類似 / ○森園 明範 (九州大学) [概要]
有理整数環におけるオイラー素数は, ある特殊な性質をみたす素数として定義され, その構成には有理整数環の商体である有理数体の二次拡大の類数が関係している. 有理整数環と類似した代数構造を持つ例として, 体上で定義された 1 変数多項式環がある. 多項式環においても, その商体である有理関数体の二次拡大の類数を考えることができる. そこで, 体上の多項式環においても, 有理関数体の二次拡大を調べることで, オイラー素数に類似する多項式を構成できるのではないかと考えた. 本講演では, 体上で定義された多項式環において, オイラー素数に類似する特殊な多項式の定式化と具体例を与える.
- 超特異ドリンフェルト加群を勘定する超特異多項式 / ○長谷川 武博 (滋賀大学教育学部) [概要]
ドリンフェルトモジュラー曲線 X はドリンフェルト加群でパラメトライズされ,超特異点は超特異ドリンフェルト加群に対応しています.
本講演では,超特異ドリンフェルト加群を勘定するドイリング多項式の形が明示的に予想できましたので,
素イデアルの次数が低い場合に,数値実験にてこの予想が正しいことをご報告させていただきます.
- MaCaulay2 Miuraパッケージの開発と今後 / ○鈴木 譲 (大阪大学) [概要]
数式処理ソフトウェアMacaulay2で、Miuraという名称のパッケージを開発し、バージョン1.9から利用可能となった。定義方程式が三浦標準形(楕円曲線のWeirstrass方程式を閉リーマン面に拡張したもの)で与えられたときの演算を処理するもので、最初のバージョンでは、ヤコビ群の演算が可能になっている。同様の処理は、他の汎用言語を用いて実現可能であるが、Miuraでは、Groebner基底の処理が基本になっていて、Macaulay2との相性がよく、ヤコビ群の演算でも
短いステップ(10行以内)で記述されている。今後は、与えられた方程式が三浦標準形か否かを判定する関数、完全交叉であるか否かを判定する関数、シグマ関数を計算する関数などを順次開発していく予定である。
▷ [研究部会OS] 数論アルゴリズムとその応用(2) [9月12日:15:00-16:20:3F](座長:長尾 孝一(関東学院大学))
- p=(3V^2+1)/4を持つ合成数の楕円曲線法による素因数分解 / ○白勢 政明 (公立はこだて未来大学) [概要]
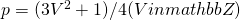 という形の素因数を持つ合成数
という形の素因数を持つ合成数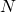 に対して、適切なパラメータを用いる楕円曲線法(ECM)と呼ばれる素因数分解法により、
に対して、適切なパラメータを用いる楕円曲線法(ECM)と呼ばれる素因数分解法により、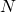 の約数(
の約数(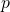 の倍数)が高速に見つかることを示す。
の倍数)が高速に見つかることを示す。
- ある素点でのみ悪い還元を持つ代数体上の楕円曲線のねじれ点について / ○安田 雅哉 (九州大学マス・フォア・インダストリ研究所) [概要]
代数体上の楕円曲線における素数位数のねじれ点の非存在性について、これまで多くの研究者により研究されてきた。具体的には、有理数体上についてMazur(1977)、2次体についてKenku-Momose(1988)と Kamienny(1992)がある素数位数のねじれ点の非存在性を明らかにした。また近年では、Kamienny-Stein-Stoll(2010)が3次体について、Derickx(2012)が4次拡大以上の代数体について、計算機による計算結果を利用してねじれ点の非存在性に関する研究成果を示した。本講演では、ある素点でのみ悪い還元を持つ楕円曲線に限定した場合の素数位数のねじれ点の存在性・非存在性に関する研究成果を紹介する。特に、代数体上ほとんどすべての素点で良い還元を持つ楕円曲線が素数位数pの位数のねじれ点を持つとき、ある代数体の類数がpで必ず割れる可除性を示すと共に、2次体上のいくつかの具体的な楕円曲線の数値例も紹介する。
- 整数計画法による格子最短ベクトル探索問題の解読報告 / ○安田 雅哉 (九州大学マス・フォア・インダストリ研究所), 脇 隼人 (九州大学マス・フォア・インダストリ研究所) [概要]
近年、高機能かつ効率的な暗号方式を構成するために格子理論が利用されている。格子を利用した暗号方式の安全性は、格子の最短ベクトルや最近似ベクトルの探索問題の計算量困難性に基づいている。特に、格子の最短ベクトル探索問題はShortest Vector Problem (SVP)と呼ばれ、与えられた格子基底から原点に最も近い格子点を探索する問題で、最悪計算量でNP困難であることが証明されている。SVPに対する解読法として、格子縮約・数え上げ・篩・random samplingの4手法、又はその組み合わせが代表的であるが、本講演ではSVPを最適化問題に変換して解読する方法を紹介する。具体的には、格子ベクトルの2乗ノルムを目的関数とし、その目的関数を最小化する解を求める最適化問題に変換し、最適化エンジンCPLEXで解読した実験結果を報告する。特に、Darmstadt大学が公開しているSVP問題に対して、CPLEXで解読できる格子次元の限界値を見積もると共に、seedが異なるSVP問題の最小解の散らばり方とその散らばり方によるCPLEXの計算時間の違いについて報告する。
- ◎円分体に対するイデアル格子上の短い生成元の復元可能性について / ○奥村 伸也 (公益財団法人九州先端科学技術研究所), 安田 雅哉 (九州大学マス・フォア・インダストリ研究所), 高木 剛 (九州大学マス・フォア・インダストリ研究所) [概要]
現在までに、円分体上のイデアル格子を利用した耐量子性に加えて完全準同型性や多重線形性を持つ高機能暗号がいくつか構成されている。それらの中には、秘密鍵として円分体のある単項イデアルの短い生成元を利用し、公開鍵からその単項イデアルの整基底が得られるものがある。そのような暗号では、単項イデアル問題と短い生成元の復元問題を解くことで秘密鍵を復元できる。
本講演では、暗号応用上重要な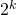 th円分体上の短い生成元の復元問題に関して、既に知られている攻撃の適用範囲の拡張法とその攻撃に対して安全な短い生成元の構成法の概要を述べる。
th円分体上の短い生成元の復元問題に関して、既に知られている攻撃の適用範囲の拡張法とその攻撃に対して安全な短い生成元の構成法の概要を述べる。
▷ [研究部会OS] 数論アルゴリズムとその応用(3) [9月12日:16:30-17:50:3F](座長:横山 俊一(九州大学))
- ◎Full Cryptanalysis of Hash Functions Based on Cubic Ramanujan Graphs / ○Jo Hyungrok (Kyushu University), Petit Christophe (University of Oxford), Takagi Tsuyoshi (Kyushu University) [概要]
Cayley hash functions are a family of cryptographic hash functions
constructed from Cayley graphs, with appealing properties such as a
natural parallelism and a security reduction to a clean, well-defined
mathematical problem. As this problem involves non-Abelian groups, it is
a priori resistant to quantum period finding algorithms and Cayley hash
functions may therefore be a good foundation for post-quantum
cryptography. Four particular parameter sets for Cayley hash function
have been proposed in the past, and so far dedicated preimage algorithms
have been found for all of them.
These algorithms do however not seem to extend to generic parameters,
and as a result it is still an open problem to determine the security of
Cayley hash functions in general.
In this paper, we study a new set of parameters for the Cayley hash
construction, corresponding to Chiu's Ramanujan graphs. We design a
polynomial time preimage attack against the resulting Cayley hash
function, showing that these particular parameters like the previous
ones are not suitable for the construction. We extend our attacks on
hash functions based on similar Cayley graphs as Chiu's Ramanujan graphs.
On the positive side, we then suggest some guidelines to select
parameters that may not be affected by this type of attacks. Our results
contribute to a better understanding of the hard problems underlying the
security of Cayley hash functions.
- ZHFEに対する選択暗号文攻撃 / ○橋本 康史 (琉球大学) [概要]
HFEは拡大体上の高次の1変数多項式を基に構成された多変数多項式暗号のひとつである.この暗号は,ランク攻撃に対する安全性を確保するために,多項式の次数を大きくする必要があり,そのため復号があまりはやくないという欠点がある.最近PQCrypto2014で提案されたZHFEでは,復号に使う拡大体上の多項式を工夫することにより,ランク攻撃を含むHFEの既存の攻撃法に対する安全性を高めることに成功した.本講演では,選択暗号文攻撃に対するZHFEの安全性が,HFEのランク攻撃に対する安全性と同じ程度であることがわかったので,その具体的な攻撃法を説明する.
▷ [研究部会OS] メッシュ生成・CAE [9月14日:16:30-17:50:1A](座長:片岡 一朗((株)日立製作所))
- 金属三次元プリンタにおける積層方向自動決定技術の検討 / ○濱口 崇志 ((株)日立製作所 機械イノベーションセンタ), 小野寺 誠 ((株)日立製作所 機械イノベーションセンタ), 青田 欣也 ((株)日立製作所 材料イノベーションセンタ) [概要]
- Lp-Delaunay図のp=2の周辺におけるメッシュ形状最適性の実験的多面評価 / ○岩本 龍馬 (和歌山大学大学院), 今井 敏行 (和歌山大学) [概要]
Lp-Delaunay図はp=2で最小角最大・最大外接円最小という規準でメッシュ形状最適性をもつことが証明されている。そのため、一般のpについては形状評価が十分に調べられていない。本研究では、p=2の周辺で上記規準での形状評価を行い、加えて他の複数のメッシュ形状評価規準においても評価実験を行った。
- ◎多視点ワイヤーアートの生成 / ○鈴木 廉 (中央大学大学院 理工学研究科 情報工学専攻), 森口 昌樹 (中央大学 理工学部 情報工学科), 今井 桂子 (中央大学 理工学部 情報工学科) [概要]
本研究では,二つの線画を,それぞれ異なる視点位置ごとにワイヤーを用いて実現するワイヤーアートの生成を行う.二つの線画と二つの視点位置を入力,ワイヤーフレームを出力とする.連結なワイヤーフレームによって,実現可能かどうかの判定を行う.また実現可能な場合,辺数最大および最小のワイヤーフレームを計算し,比較する.
▷ [研究部会OS] 離散システム(1) [9月13日:09:30-10:50:3E](座長:平井 広志(東京大学))
- ◎距離空間と最小全域木のフィッティングの良さをはかる尺度の構築にむけて / ○早水 桃子 (総合研究大学院大学(統計数理研究所)) [概要]
有限集合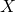 上の距離
上の距離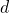 がtree metricであるとは,距離空間
がtree metricであるとは,距離空間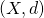 を実現する
を実現する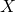 上のpartially labelled treeが存在することをいう.四点条件はtree metricを特徴づける(不)等式の形をした条件であり,その最大の逸脱度として定義される
上のpartially labelled treeが存在することをいう.四点条件はtree metricを特徴づける(不)等式の形をした条件であり,その最大の逸脱度として定義される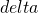 -hyperbolicityは距離空間と系統樹のフィッティングの良さをはかる尺度として機能する.一方,本講演では,距離空間と最小全域木のフィッティングの良さをはかる計算しやすい尺度の構築を目指して四点目条件という新しい条件を導入し,この四点目条件を主役にして
-hyperbolicityは距離空間と系統樹のフィッティングの良さをはかる尺度として機能する.一方,本講演では,距離空間と最小全域木のフィッティングの良さをはかる計算しやすい尺度の構築を目指して四点目条件という新しい条件を導入し,この四点目条件を主役にして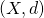 を実現する
を実現する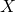 上のfully labelled treeが存在するための必要十分条件を述べる.
上のfully labelled treeが存在するための必要十分条件を述べる.
- ◎一般の遷移確率に対する決定性ランダムウォークの全訪問時間 / ○白髪 丈晴 (九州大学大学院システム情報科学府) [概要]
決定性ランダムウォーク(deterministic random walk)とは, ランダムウォークを模倣しうる決定的過程である. これまで, 単純ランダムウォークに対応するロータールーターモデルと呼ばれる決定性ランダムウォークの全訪問時間(グラフ上の全頂点を探索するのにかかる時間)に対し多くの既存研究が為されている. 本研究では一般の遷移確率に対応する決定性ランダムウォークに対し初の全訪問時間の上界を導出した. また, この上界は既存のロータールーターモデルの上界を改善している.
- ◎系列二分決定グラフを用いた文字列集合演算 / ○伝住 周平 (東京大学) [概要]
系列二分決定グラフは有限な文字列集合をコンパクトに表現できるデータ構造である.また,和集合や積集合,差集合など文字列集合同士の基本的な演算をサポートしている.本講演では,文字列集合の乗除・剰余や部分文字列・近似文字列の列挙といったより複雑な演算を系列二分決定グラフ上で実現するアルゴリズムを紹介する.
- 部分木距離の表現を見出すためのアルゴリズム / ○安藤 和敏 (静岡大学工学部), 佐藤 公紀 (株式会社大都技研) [概要]
写像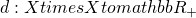 は,もし重み付き木
は,もし重み付き木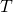 と
と
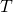 の部分木の集合
の部分木の集合 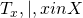 が存在して各
が存在して各
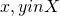 に対して
に対して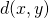 が
が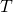 の中における
の中における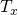 と
と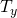 の距離に等し
いならば,部分木距離と呼ばれる.
与えられた部分木距離に対してそれを表現する木と部分木の集合を見出す多項式時間アルゴリズム
はこれまで知られていなかった.本研究では,与えられた部分木距離の表現を見出す
O
の距離に等し
いならば,部分木距離と呼ばれる.
与えられた部分木距離に対してそれを表現する木と部分木の集合を見出す多項式時間アルゴリズム
はこれまで知られていなかった.本研究では,与えられた部分木距離の表現を見出す
O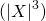 時間アルゴリズムを示す.
時間アルゴリズムを示す.
▷ [研究部会OS] 離散システム(2) [9月13日:11:00-12:20:3E](座長:小林 祐輔(筑波大学))
- ◎動画広告割当のオンライン最適化 / ○澄田 範奈 (国立情報学研究所), 河瀬 康志 (東京工業大学), 藤田 澄男 (Yahoo! JAPAN研究所), 福永 拓郎 (国立情報学研究所) [概要]
本研究では動画広告をユーザーに割当てることによる広告収入を最大化する問題を扱う.動画広告はインターネット広告の一種であり,現在急速に利用が広まっている.従来のインターネット広告の割当問題には様々な関連研究が存在するが,動画広告では重要な,広告が視聴される時間枠を扱っているものはない.本研究では,先行研究を拡張し,動画広告割当にも使用できる競合比(1-1/e)のオンラインアルゴリズムを提案する.
- ◎2部グラフのDM既約化 / 岩田 覚 (東京大学), 加藤 純 (トヨタ自動車株式会社), ○山口 勇太郎 (大阪大学) [概要]
2部グラフのDM分解は,最大マッチング全体の構造を反映した,頂点集合の一意な分割を与える.
DM分解がただ1つの成分のみからなるような2部グラフを,DM既約であるという.
本講演では,「与えられた2部グラフをDM既約にするような最小の追加枝集合」を求める,簡潔な組合せ的アルゴリズムを提案する.
- イマージョンを含まないグラフに対する彩色アルゴリズム / ○垣村 尚徳 (東京大学), 河原林 健一 (国立情報学研究所) [概要]
グラフのイマージョンは,マイナーや細分のようにグラフの包含関係を表す概念であり,グラフのマイナーと良く似た性質を持つことが知られている.本講演では,グラフ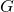 が,最大次数
が,最大次数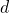 のグラフ
のグラフ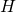 をイマージョンとして持たないときに,
をイマージョンとして持たないときに,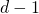 彩色可能かを判定するアルゴリズムを提案する.このアルゴリズムは
彩色可能かを判定するアルゴリズムを提案する.このアルゴリズムは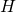 のサイズをパラメータとした固定パラメータアルゴリズムである.
のサイズをパラメータとした固定パラメータアルゴリズムである.
- 地域コミュニティ構造の変化に対する尤度比検定 / ○谷口 隆晴 (神戸大学), 河崎 素乃美 (中京テレビ放送), 増本 康平 (神戸大学), 近藤 徳彦 (神戸大学), 岡田 修一 (神戸大学) [概要]
高齢化地域の抱える問題の解決のため,発表者らは住民ネットワーク形成に関する行動科学的手法の研究とその効果を検証するための統計的検定法について研究を進めてきた.本発表では,特に,ネットワークモデルとしてランダムグラフを用いた尤度比検定について報告する.
▷ [研究部会OS] 離散システム(3) [9月13日:13:30-14:50:3E](座長:萩田 真理子(お茶の水女子大学))
- ◎ユニモジュラ変換による微分代数方程式の指数減少法 / 岩田 覚 (東京大学), ○高松 瑞代 (中央大学) [概要]
指数の高い微分代数方程式(DAE)の数値計算では,指数減少法を適用して得られるDAEを解くのが一般的である.現在の数値計算ソフトウェアに導入されているPantelidesのアルゴリズムはグラフ理論を用いた高速な手法である一方で,数値情報を捨象しているため結果が正しいとは限らないという大きな問題点がある.この問題点を解決するために,本研究ではグラフ理論と数値計算を融合したDAEの指数減少法を提案する.
- 閉路の存在性に関する定理の関係について / ○山下 登茂紀 (近畿大学理工学部) [概要]
日本人を含め多くの研究者によって,グラフが閉路や木構造を部分構造として含むための次数和条件が与えられている.しかし,残念ながら,これらの定理の関係性についてはあまり議論されてこなかった.本講演では,次数和条件に関する定理を紹介するとともに,それらの定理の関係性について述べる.
- NISTの二重検定における適切なサンプル数の決定 / ○原本 博史 (愛媛大学), 松本 眞 (広島大学) [概要]
擬似乱数の統計的検定では、しばしば二重検定が用いられる。この講演では、2つの確率分布の食い違いを測る量である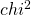 -discrepancyを用いて、第1段階のサンプル数に応じた適切な第2段階の検定のサンプル数を決定する方法を紹介する。特にNISTで実装されているいくつかの検定について、上記のサンプル数の計算方法と実験結果を紹介する。
-discrepancyを用いて、第1段階のサンプル数に応じた適切な第2段階の検定のサンプル数を決定する方法を紹介する。特にNISTで実装されているいくつかの検定について、上記のサンプル数の計算方法と実験結果を紹介する。
- 単体的複体の分割可能性とh-triangle / ○八森 正泰 (筑波大学システム情報系) [概要]
単体的複体の分割可能性という性質と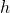 -triangleとの関連を中心に、関係する諸性質との関係を紹介し、
-triangleとの関連を中心に、関係する諸性質との関係を紹介し、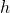 -triangleを単体的複体が分割可能でないことを示す手段として用いる可能性、特に、hereditary-propertyについての問題との関連について議論する。
-triangleを単体的複体が分割可能でないことを示す手段として用いる可能性、特に、hereditary-propertyについての問題との関連について議論する。
▷ [研究部会OS] 連続体力学の数理(1) [9月14日:09:30-10:50:1A](座長:平野 史朗(立命館大理工))
- [40分講演] 安定化非圧縮性SPH法の精度検証と妥当性確認 / ○浅井 光輝 (九州大学) [概要]
SPH法により非圧縮性流体を解くには、これまでに射影法を適用し圧力のみを陰的に解くISPH法と、圧力を定義する状態方程式を別途定義することで圧力についても陽的に積分するWCSPH法が存在している。前者は圧力の精度については後者に勝るものの、ポアソン方程式を解く必要があり、計算時間に関しては後者が有利とされている。
本研究では、ポアソン方程式を解くSPH法を採用し、その改良案を提示し、その精度検証と妥当性確認の結果を報告する。また、最近開発中の陽的ISPH法についても現状の性能について報告する。
- ◎生体粘弾性モデルに対する非適合三角形有限要素法による高精度計算 / ○前川 秀 (京都大学大学院 情報学研究科) [概要]
生体を加振した際に生じる弾性波は,Time-harmonicな粘弾性方程式により記述される.この方程式に通常の有限要素法を適用すると,得られる近似解の精度は期待される精度に比べて著しく悪いものになる.本講演では,このモデルに対して非適合有限要素法を用いることを提案し,その有効性を数値計算例により示す.
- Maxwell流体に対するフェーズフィールドき裂進展モデルの拡張 / ○高石 武史 (広島国際学院大学), 田中 良巳 (横浜国立大学) [概要]
高石と木村によって導出されたフェーズフィールドを用いたき裂進展モデルは,き裂の進展に伴うメッシュの切り直しや計算領域の変更,き裂先端部での応力集中の緩和など,数値計算に適した多くの性質を持っており,実際の数値計算においても,破壊靭性分布に対応したき裂進展やき裂の融合・分枝といった現象も再現できている.その他にも,このモデルはシンプルな導出方法のために拡張が容易であり,水素分子の拡散に伴う脆化現象にも適用されている.本研究では,このモデルのベースとなる Bourdin-Francfort-Marigo のエネルギー表式に内部歪み変数を導入することで, Maxwell 流体におけるき裂進展現象を扱うモデルを導出した.ここでは,Maxwell 流体の持つダンパーとしての性質が内部歪みとして扱われ,内部歪はダンパーの粘性係数に従った時間変化を行う.材質の変位をスカラー変数で表せるモードIII型のせん断き裂のモデルの数値計算結果では,き裂の進展に関して粘性係数の閾値が現れることがわかった.今後,このモデルを拡張・改良していくことで粘弾性体におけるき裂進展現象を調べていくことが期待される.
▷ [研究部会OS] 連続体力学の数理(2) [9月14日:11:00-12:20:1A](座長:高石 武史(広島国際学院大学))
- [40分講演] ◎粘弾性変形の大規模有限要素解析を用いた地殻構造最適化手法の開発 / ○縣 亮一郎 (東京大学大学院工学系研究科), 市村 強 (東京大学地震研究所), 堀 高峰 (海洋研究開発機構), 平原 和朗 (京都大学大学院理学研究科), 橋本 千尋 (名古屋大学大学院環境学研究科), 堀 宗朗 (東京大学地震研究所) [概要]
海溝型巨大地震発生後の数年間における地殻変動は,一般的に粘弾性体における準静的な変形として計算される.本発表では,地震後地殻変動の高分解能計算を可能にする,粘弾性変形の大規模有限要素解析手法について述べる.その後,この解析手法とアジョイントベースの最適化を組み合わせて地殻変動観測データからの地中粘性パラメータ推定を行い,地殻構造モデルを高度化していくための試みについて述べる.
- 地震時の断層滑りの空間不均質と地震波の高周波成分、各々を特徴づけるパラメタ間の関係 / ○平野 史朗 (立命館大理工) [概要]
地震は地殻内に蓄えられた弾性歪みエネルギーを解放する現象である.
解放されたエネルギーの一部は弾性体の破壊と摩擦仕事に消費され, 残りは弾性波すなわち運動エネルギーへと変換される.
これらエネルギーの記述に必要なパワースペクトル密度関数 (PSD) の経験的モデル化は, 観測事実を基に提唱されている.
本研究では, これら経験則に基づく PSD を内包する数理モデルを考察する.
- 氷河で観測される剣山状突起物の数理モデルの提案とその3Dシミュレーション / ○加藤 純平 (金沢大学大学院 自然科学研究科 数物科学専攻), 木村 正人 (金沢大学 理工研究域 数物科学系) [概要]
アンデス山脈やヒマラヤ山脈などの特定の地域の氷河ではペニテンテと呼ばれる剣山状の氷の構造物が観測される.本研究では,その構造物の数理モデルを考え,実際にシミュレーションをすることでその解の動向を調べる.
▷ [研究部会OS] 連続体力学の数理(3) [9月14日:13:30-14:50:1A](座長:木村 正人(金沢大学 理工研究域 数物科学系))
- Stability analysis of Sompolinsky’s primary visual cortex model / ○本多 泰理 (NTTネットワーク基盤技術研究所) [概要]
Sompolinskyによる脳の一次視覚野の神経発火モデルについて、Full modelの定常解導出と安定性解析に関する議論を行う。
- 最小コンプライアンス,仕事関数の劣微分の変分不等式解と関連の発展方程式の漸近解の関係 / ○海津 聰 (東京理科大学) [概要]
最小コンプライアンス問題は仕事関数の最小値を与える領域の
最適密度を求める問題である.この最適密度は仕事関数の
劣微分作用素を施すと零値をとる.又,劣微分作用素に対応する時間発展方程式
の漸近解でもあることを明らかにする.
- 3次元Helmholtz方程式の周期境界値問題における多重極法とSakurai-Sugiura法を用いた固有値解析 / 山本 貴也 (京都大学情報学研究科), 新納 和樹 (京都大学情報学研究科), ○西村 直志 (京都大学情報学研究科) [概要]
フォトニック結晶やメタマテリアルに関連して現れる3次元Helmholtz方程式の周期境界値問題の固有Floquet波数に関する固有値問題を,周期多重極法とSakurai-Sugiura法を用いて解く数値計算法について述べる.
- 一般J積分による特異点集合の形状最適化について / ○大塚 厚二 (広島国際学院大学) [概要]
偏微分方程式境界値問題における解の特異点集合について,エネルギー,最小2乗誤差,平均コンプライアンスをコスト関数とする形状最適化について報告する.ここでの特異点集合は,偏微分方程式を定義する領域の境界,混合境界条件の接合部,不連続係数のつくる界面などから構成される.
-
Origami-performing robot: The optimization of geometrical design of a robot gripper / ○THAI PHUONG THAO (Graduate School of Advanced Mathematical Sciences, Meiji University), SAVCHENKO MARIA (Graduate School of Advanced Mathematical Sciences, Meiji University), HAGIWARA ICHIRO (Graduate School of Advanced Mathematical Sciences, Meiji University) [概要]
Gripping is a key task for robotic arms. The crease line length in forming process by the robot arms can be limited by the gripper sizes. Based on this, we consider an optimization of the geometry of the plane contact portion of gripper for forming the crease line with a given length. Required forces are applied to the object surface via a contact portion of the gripper. The target of this investigation is to define the tensile force configurations and design the plane contact portion of the robotic gripper for forming the sharp crease lines in the origami crease pattern without wrinkles on a sheet of paper. For solving this problem we apply a pure plane geometrical approach. The geometrical algorithm is described and illustrated with drawings.
-
コンパクトな折り紙へルメットの衝撃特性 / ○楊 陽 (明治大学), 奈良 知惠 (明治大学), 萩原 一郎 (明治大学) [概要]
地震や自転車事故の際,安全を守る最も身近なものの一つに安全ヘルメットや安全帽子がある。 特にヘルメットの場合,教室内に置くと通路が狭くなり,ロッカーに入らないという事態も生じている。これを解決すべく折り畳みのヘルメットが期待される。コンパクト収納に優れと保護規格を満足のため,折紙工学を推進する折紙の展開収縮機能の利用と衝突研究が検討される。
-
マクスウェル粘弾性体モデルの勾配流構造と有限要素解析 / ○山本 大輝 (金沢大学), 木村 正人 (金沢大学), 田中 良巳 (横浜国立大学), 野津 裕史 (金沢大学) [概要]
マクスウェル粘弾性体モデルの問題を、弾性体問題における応力、歪みの式から新たに粘性部分の応力、歪みを定義することで導出し、この問題のエネルギー勾配流構造及び有限要素解析の結果を示す。
-
フェーズフィールドモデルを用いた3次元弾性体における亀裂進展の3Dシミュレーション / ○中野 匠 (金沢大学) [概要]
以前より、老朽化・疲労破壊によって物体に入った亀裂がどのように進展するかは安全性の確認の上で重要な問題とされてきた。今回は3次元弾性体に関して、境界値問題を有限要素法で解くプログラミングソフト『FreeFem++』と可視化ツール『FFIsoVis』を使い、フェーズフィールド時間発展モデルを用いた亀裂進展の3Dシミュレーションを行っていく。
-
Applications of Computational Topology to Medical Science / ○寺本 敬 (旭川医大) [概要]
We have implemented and tested a methodology based on computational homology for medical science. Betti numbers are one of the topological invariants counting the number of geometrical objects and persistent homology measures the robustness of holes against noise for images. We report our trials to apply this mathematical tool to characterize the bone porosity and immunohistochemical scoring for scanned image data.
-
KMATHLIB -High Performance and Scalable Numerical Library for the K Computer- / ○大井 祥栄 (理化学研究所計算科学研究機構), 廣田 悠輔 (理化学研究所計算科学研究機構), 椋木 大地 (理化学研究所計算科学研究機構), 今村 俊幸 (理化学研究所計算科学研究機構) [概要]
我々のチームでは京コンピュータを代表とする大規模汎用計算機における数値計算ライブラリのためのフレームワーク”KMATHLIB”を開発している.KMATHLIBは統合的なインターフェース“KMATHLIB API”を含んでおり,高並列・高性能なライブラリ利用を容易にする.本発表ではKMATHLIBの特徴を概説し,KMATHLIB APIを用いる利点等について詳しく述べる.
-
浅水波方程式のためのLagrange-Galerkinスキームの開発 / ○二井 滉太 (金沢大学理工学域数物科学類), 野津 裕史 (金沢大学理工学域数物科学系准教授) [概要]
津波の支配方程式である浅水波方程式のためのLagrange-Galerkinスキームを提案する.
提案スキームにおいて数値的な誤差が収束することを示し、波が伝わる様子を数値シミュレーションで確認する.
-
C-PLANEネットワークへの概周期周波数配置の適用 / ○中澤 勇夫 (京都大学情報学研究科), 梅野 健 (京都大学情報学研究科) [概要]
5世代移動通信(5G)では2020年運用開始を目標に大容量化・信頼性と共に多重アクセスを目指して試験開発が進められている。
5世代でのHeterogeneous Networkには各Homogeneous Networkを制御するC-PLANE (Control plane)が重要な役割を負うっている。
本研究ではC-PLANEに従来から研究を進めている概周期周波数配置(APFA)を適用して通信システムの性能評価の報告を行うもので、APFAによる10万CH以上のマルチユーザ収容と、制御信号の送受信時の変復調処理と10万CH間の隣接干渉のシミュレーションを行い、BER特性についての結果を報告する。
-
最大同種1対2マッチング問題 / ○天野 立義 (同志社大学大学院理工学研究科), 泉 裕紀 (同志社大学大学院理工学研究科), 渡辺 扇之介 (京都府立大学生命環境学部), 渡邊 芳英 (同志社大学理工学部) [概要]
本講演では最大同種1対2マッチング問題について考察する.
通常個別指導塾では講師1人に生徒が2人つき,指導が1対2で行われている.
最大同種1対2マッチング問題とは,例えば理系と文系のグループがあるときに指導内容が重なるよう,講師1人と文系生徒2人の対,あるいは講師1人と理系生徒2人の対の合計なるべく多く作る問題をモデルとして考えたものである.
-
曲率流方程式に対する差分スキームの誤差収束への試み / ○小林 広典 (金沢大学大学院 自然科学研究科), 木村 正人 (金沢大学 数物科学系) [概要]
曲率流方程式に対する差分スキームの誤差収束について数値解析的・数学的に考察することにより,誤差が収束しているかを確認するための研究テーマである.今回は初期曲線を楕円として考えて誤差の数値解析を行い,さらに数学的な誤差収束の証明をするためのアイデアについて述べた.今後は実際に数値計算結果が正しいものかを数学的なアイデアを用いて確認していく.
-
◎養殖水産資源に対する最適漁獲開始時刻の支配方程式 / ○吉岡 秀和 (島根大学生物資源科学部), 八重樫 優太 (京都大学大学院農学研究科), 次橋 健太郎 (島根大学生物資源科学部) [概要]
商業目的で水産資源を人工的に飼育する養殖業は,現代の主要水産業として成立している.養殖業の経済性を追求する場合,水産資源や飼育手法の種類に応じた漁獲戦略が要求される.本研究では,我が国の主要水産資源である「アユ」を対象に,既知の漁獲圧と飼育コストのもとで最適漁獲開始時刻の支配方程式を導く.また,最適漁獲開始時刻の一意存在性と比較静学に関する数学解析結果を斐伊川漁業協同組合の実例を交えて紹介する.
-
◎非凸多面体領域におけるPoisson方程式の有限要素法の
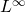 評価 / ○千葉 悠喜 (東京大学大学院数理科学研究科), 齊藤 宣一 (東京大学大学院数理科学研究科) [概要]
評価 / ○千葉 悠喜 (東京大学大学院数理科学研究科), 齊藤 宣一 (東京大学大学院数理科学研究科) [概要]
適当な条件をみたす3次元多面体領域に対し,離散調和関数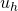 は
は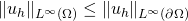 を満たす.これを用いることで,条件を満たす非凸多面体領域における有限要素法の
を満たす.これを用いることで,条件を満たす非凸多面体領域における有限要素法の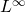 評価が得られる.本発表では,証明の概略と数値例を示す.
評価が得られる.本発表では,証明の概略と数値例を示す.
-
◎主値積分の形状微分を用いた定常渦斑の数値計算 / ○宇田 智紀 (京都大学数学教室) [概要]
2次元Euler方程式において,渦斑は一定渦度領域をもつ基本的な解の一つである.定常渦斑問題は,時間発展に伴い渦斑境界Cが変化しない解を求める問題であり,C上の主値積分で書かれる零点問題F(C)=0に帰着できる.数学解析・数値解析では,未知形状に関する形状微分が重要と考えられ,主値積分の積分路に関する形状微分公式を導出した.講演では,様々な問題設定における数値計算結果も紹介する.
-
◎弦とボディの連成シミュレーションによるギターのサウンドレンダリング / ○長谷阪 祐太 (神戸大学 大学院 システム情報学研究科), 谷口 隆晴 (神戸大学 大学院 システム情報学研究科) [概要]
サウンドレンダリングとは,物理現象とそれに伴う音について同時にシミュレーションし,リアリティのある音付きの動画を作成することを目指した分野である.
本研究では,ギターのサウンドレンダリングを目標とし,その準備として,弦とボディの連成シミュレーションを行った.本発表では,その結果について報告する.
-
◎B-splineによる時間変数近似の逐次的構成の解析 / ○上田 祐暉 (東京大学数理科学研究科), 齊藤 宣一 (東京大学数理科学研究科) [概要]
時間発展偏微分方程式の近似解法の一つであるspace-time法は, 狭義には時間変数の離散化に不連続Galerkin法を用いるものであり, 時間変数に関する高精度化を実現している. しかしその不連続性は, 実現象のシミュレーションの際に不都合になり得るため, B-splineを用いた逐次近似によりこれを解消する手法が提案されている. 本発表では, その逐次近似手法に関する数学的な結果の最新のものを紹介する.
-
◎振動による接着剥離の数理モデルと有限要素シミュレーション / ○米田 拓朗 (金沢大学) [概要]
本研究では,R.Scala(2015,preprint)の剥離モデルについて,有限要素法を用いた計算方法の提案と,シミュレーションを行った.ある二つの弾性体が接着面で結合しているものとし,外力を与えたときにどの様に力が伝わり,剥離がおきるかについての問題を考察した.
-
◎衝突・分裂を許容する四方・六方対称クリスタライン法と2次元雪結晶モデル / ○山岡 良平 (金沢大学大学院自然科学研究科), 田中 智恵 (金沢大学大学院自然科学研究科) [概要]
本研究では,雪の結晶成長のように辺の衝突や分裂を許容する,2次元結晶成長モデルの数学的枠組みの構築を目指している.田中智恵(2016,
修論)で考えられた六角形結晶を元に,四角形成長モデルを考えており,このモデルについて数値計算を行った.
-
◎ε-Stokes問題:圧力境界条件を含んだStokes方程式の境界値問題 / ○松井 一徳 (金沢大学 理工学域数物科学類) [概要]
流速のみの境界条件が与えられたStokes方程式は一意的な解を持ち,その性質はよく知られている.しかし圧力境界条件を含んだ境界値問題についての解析的な議論はあまりない.ここでは圧力Poisson方程式を用いて解く方法の正当性についてdiv-freeでない流速の例などを通して考察する.
-
◎離散ハングリー戸田格子の非自励化について / ○前田 一貴 (関西学院大学) [概要]
双直交多項式のスペクトル変換からいくつかの関係式を作り,それらの両立条件を考えると非自励離散ハングリー戸田格子の減算を含まない漸化式が容易に得られることを報告する.また,得られた漸化式の応用について考える.
-
◎一次元領域における非線形拡散項を伴う方程式の定常解に対する精度保証付き数値計算法 / ○木村 翔矢 (早稲田大学大学院基幹理工学研究科), 関根 晃太 (早稲田大学理工学術院), 大石 進一 (早稲田大学理工学術院) [概要]
一次元空間内の有界領域上の非線形反応拡散方程式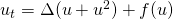 にDirichlet境界条件を課した場合の定常解に対して、Newton-Kantorovichの定理を用いた精度保証付き数値計算法を提案する. この方程式は、拡散項に
にDirichlet境界条件を課した場合の定常解に対して、Newton-Kantorovichの定理を用いた精度保証付き数値計算法を提案する. この方程式は、拡散項に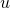 に関する非線形関数を含むことが特徴であり、数理生態学における交差拡散競合系など、種々の数理モデルの解析への応用が期待できる.
に関する非線形関数を含むことが特徴であり、数理生態学における交差拡散競合系など、種々の数理モデルの解析への応用が期待できる.
-
◎一般内積に対するグラム・シュミット直交化の効率的実装法の提案およびその性能評価 / ○今倉 暁 (筑波大学), 山本 有作 (電気通信大学) [概要]
本講演では,正定値対称行列 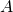 により定められる一般内積に対し,グラムシュミット直交化による長方行列のthin QR分解について考える.一般内積に対するグラムシュミット直交化は,標準内積に対するグラムシュミット直交化の自然な拡張として導出することができる.本講演では,行列
により定められる一般内積に対し,グラムシュミット直交化による長方行列のthin QR分解について考える.一般内積に対するグラムシュミット直交化は,標準内積に対するグラムシュミット直交化の自然な拡張として導出することができる.本講演では,行列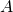 に対する行列ベクトル積の回数に着目し,効率的実装法を提案する.また,誤差解析および数値実験から提案法の性能評価を行う.
に対する行列ベクトル積の回数に着目し,効率的実装法を提案する.また,誤差解析および数値実験から提案法の性能評価を行う.
-
◎Python上での区間演算の高速な実装について / ○浅見 和哉 (早稲田大学 基幹理工学部研究科), 柏木 雅英 (早稲田大学 理工学術院) [概要]
概要 近年、Pythonを利用した数値計算の利用が急速に増えている。しかし、 Pythonにおいてよく知られた精度保証付き数値計算のライブラリは存在しない。本研究ではPython上で発生する問題を解決しつつ、精度保証ライブラリの核となる方向付き丸め計算を複数の方法で実装し、速度を比較した。その結果、C言語の関数をPython上から呼び出すものが最速となった。今後は行列計算での区間型の実装を目標としていく。
-
◎粒子エネルギーの勾配流と平衡状態 / ○楊 振興 (金沢大学) [概要]
Let  be a bounded domain in
be a bounded domain in  and we consider
and we consider 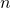 particles
particles 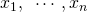 in
in 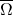 . We set
. We set 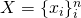 and call
and call 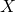 a particle distribution. We define
a particle distribution. We define 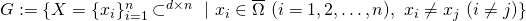 and energy of particles
and energy of particles 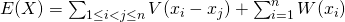 which consists of interactive energy
which consists of interactive energy 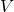 and self-energy
and self-energy 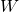 . In this lecture, I consider in 1-dimension, the problem is to find a
. In this lecture, I consider in 1-dimension, the problem is to find a 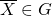 , such that :
, such that : 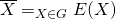 . We can show that it is a equilibrium state when
. We can show that it is a equilibrium state when 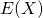 is minimum.
is minimum.
-
◎レイリー・ベナール対流に現れるラグランジュ・コヒーレント構造とカオス的混合に関する数値解析 / ○宮本 知紘 (早稲田大学), 渡辺 昌仁 (早稲田大学), 吉村 浩明 (早稲田大学) [概要]
レイリー・ベナール対流に現れる混合過程はラグランジュ的な視点から見るとカオス的な挙動を示すことが知られている.本研究では,系の大域的な秩序構造を支配するラグランジュ・コヒーレント構造を有限時間リアプノフ指数(FTLE)により計算し,カオス的な流体混合について考察する.また,ポアンカレ断面との比較からFTLE場とカオス領域及び規則領域の関係について示し,カオス的な流体混合のメカニズムを明らかにする.
-
◎離散可積分系によるNewell-Whithamモデルの時間差分化 / ○鈴木 大庸 (法政大学 大学院), 礒島 伸 (法政大学) [概要]
交通流モデルとして知られているoptimal velocity (OV) モデルと、可積分方程式であるmodified Korteweg-de Vries (mKdV) 方程式の対比により、時間離散mKdV方程式を利用したOVモデルの時間差分化が金井らによって提出されている。本発表では、交通流モデルの1つである遅延微分方程式Newell-Whitham (NW) モデルと、可積分であるKac-van Moerbeke (KvM) 系との対比に注目し、離散時間KvM系を利用したNWモデルの時間差分化を提案する。また、得られた離散時間モデルの厳密解、数値解についても議論する。
-
◎気泡のリバウンド挙動とレイリー・プレセット方程式に基づく衝撃圧の解析 / ○東田 隆祥 (早稲田大学), 實淵 泰樹 (早稲田大学), 友田 幸輝 (早稲田大学), 國島 正樹 (早稲田大学), 祖父江 聡志 (早稲田大学) [概要]
超音波による強制加振のもとで生成した単一気泡は,周期的な膨張と収縮からなるリバウンド挙動を示すことが知られている.本研究では,リバウンド挙動と気泡周囲の圧力状態を実験的に観測するとともに,レイリー・プレセット方程式に基づく数値解析を行う.特に,圧壊時に観測される衝撃圧の発生・伝播を,レイリー・プレセット方程式と1次元波動方程式の連成モデルとして表し,実験値と比較することでモデルの妥当性を検証する.
-
◎最大異種1対2マッチング問題 / ○泉 裕紀 (同志社大学大学院理工学研究科), 天野 立義 (同志社大学大学院理工学研究科), 渡辺 扇之介 (京都府立大学生命環境学部), 渡邊 芳英 (同志社大学理工学部) [概要]
本問題を考えた動機は,個別指導塾などの指導方法にある.生徒同士でも苦手分野を教えあえるように,講師1人に対して文系の生徒と理系の生徒がつき,指導が1対2で行われているとする.本講演で取り上げる最大異種1対2マッチング問題はこのような先生1人と生徒2人の対をなるべく多く作る問題をモデルとして考えたものである.本講演では,最大異種1対2マッチング問題を定義し,これに対する解法アルゴリズムを述べる.
-
◎非ホロノミック拘束を受ける力学系と離散ラグランジュ・ディラック構造 / ○百瀬 宏樹 (早稲田大学), 彭 林玉 (早稲田大学), 吉村 浩明 (早稲田大学) [概要]
拘束を受ける力学系において,数値解析の手法としてスティッフ安定なBDF法などが用いられることが多いが,長時間の数値計算においてはエネルギーに重大な誤差が発生してしまうことが問題となる.本研究では,離散ディラック構造を保存する変分的積分法の提案を行う.さらに,地面を滑らずに転がる垂直円盤の系などを例にその有効性を示すことで,新たな非ホロノミックな離散積分法の提案を行う.
-
◎KKT方程式を用いた最適化問題に対する精度保証付き数値計算法 / ○齊藤 優里香 (早稲田大学大学院基幹理工学研究科数学応用数理専攻), 柏木 雅英 (早稲田大学理工学術院) [概要]
最適化問題の精度保証付き数値計算についてはこれまであまり扱われておらず、線形・非線形問わず精度保証の手法を確立する必要があった。本研究では、非線形計画問題の最適性における1次の必要条件として知られるKKT条件を、ある方法を用いて不等式を含まない方程式に直すことによりKrawczyk法を適用できるようにする。制約付きの非線形計画問題、特に凸計画問題の例を示す。
-
◎Delaunay三角形分割の精度保証付き数値計算手法に対する考察 / ○若山 馨太 (早稲田大学), 田中 一成 (早稲田大学), 関根 晃太 (早稲田大学), 尾崎 克久 (芝浦工業大学), 大石 進一 (早稲田大学,CREST/JST) [概要]
Delaunay三角形分割の計算手法は,Divide-and-Conquer法やSweep Line法など様々なものが提案されてきた.Shewchuk氏は,これら手法の計算過程を厳密に評価するプログラムを開発した.今回は,Shewchuk氏が開発しなかったFlip法について,厳密に正しい計算が行われたかどうかを確認するプログラムを開発し,その他手法との比較を行う.
[9月12日:18:30-20:30:2B](座長:高橋 大輔(早稲田大学))
- 線形問題における精度保証付き数値計算について / ○森倉 悠介(早稲田大学 理工学術院)
- 偏微分方程式の解に対する精度保証付き数値計算法について / ○関根 晃太(早稲田大学 理工学術院)
- 可積分系と精度保証付き数値計算 / ○丸野 健一(早稲田大学 理工学術院)
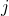 -関数はモジュラー関数の中でも最も基本的な関数である. これについて,虚数乗法論,そして Monstrous Moonshine という大きな理論が知られている. それらをおおざっぱに,それぞれ
-関数はモジュラー関数の中でも最も基本的な関数である. これについて,虚数乗法論,そして Monstrous Moonshine という大きな理論が知られている. それらをおおざっぱに,それぞれ 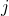 -関数の虚二次点,無限遠点での振る舞いに関して何かを言う理論だと思うとすると,もう一つ,実二次点での振る舞いはどうかというのが気になる. これらについて筆者が20年来行ってきたささやかな研究,空想についてお話ししたいと思う.
-関数の虚二次点,無限遠点での振る舞いに関して何かを言う理論だと思うとすると,もう一つ,実二次点での振る舞いはどうかというのが気になる. これらについて筆者が20年来行ってきたささやかな研究,空想についてお話ししたいと思う.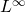 評価 / ○千葉 悠喜 (東京大学大学院数理科学研究科), 齊藤 宣一 (東京大学大学院数理科学研究科) [概要]
評価 / ○千葉 悠喜 (東京大学大学院数理科学研究科), 齊藤 宣一 (東京大学大学院数理科学研究科) [概要]
